هنگامی كه يک سيم به‌صورت مربعی به ضلع $a$ در می‌آيد، به‌ازای هر $4a$ (اندازهٔ محيط مربع)، يک دور به‌وجود می‌آيد. بنابراين تعداد دور اين مربع برابر است با:

$L=N\times 4a\Rightarrow 120=N\times 4\times 10\Rightarrow N=3$

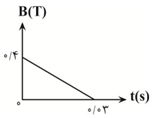
با توجه به شكل، معادلهٔ ميدان مغناطيسی برحسب زمان برابر است با: 

$B=at+b\Rightarrow \left\{ \begin{matrix} t=0,B=0/4T  \\ t=0/03s,B=0  \\ \end{matrix} \right.\to \left\{ \begin{matrix} 0/4=0+b  \\ 0=a\times 0/03+b  \\ \end{matrix} \right.$

$\Rightarrow \left\{ \begin{matrix} b=0/4T  \\ a=-\frac{40}{3}\frac{T}{s}  \\ \end{matrix}\Rightarrow B=-\frac{40}{3}t+0/4 \right.$

اندازهٔ میدان در لحظهٔ $t=0/02$ ثانيه برابر است با:

$B=-\frac{40}{3}\times 0/02+0/4=\frac{2}{15}T$

نيروی محركهٔ متوسط القا شده و جريان القايی متوسط متوسط در پيچه برابر است با: 

$\overline{\varepsilon }=-N\frac{\Delta \Phi }{\Delta t}\xrightarrow{\Phi =BA\cos (\theta )}\overline{\varepsilon }=-N\frac{{{B}_{2}}A\cos (\theta )-{{B}_{1}}A\cos (\theta )}{\Delta t}\Rightarrow \overline{\varepsilon }=-NA\cos (\theta )\frac{{{B}_{2}}-{{B}_{1}}}{\Delta t}$

$\xrightarrow{A={{a}^{2}}}\overline{\varepsilon }=-3\times {{(10\times {{10}^{-2}})}^{2}}\times 1\times \frac{\frac{2}{15}-0/4}{0/02}=0/4V$

$\Rightarrow \overline{I}=\frac{\overline{\varepsilon }}{R}=\frac{0/4}{0/1}=4A$