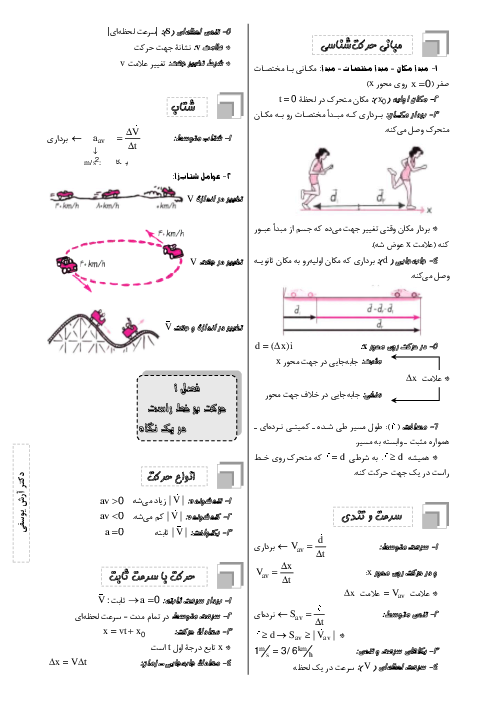
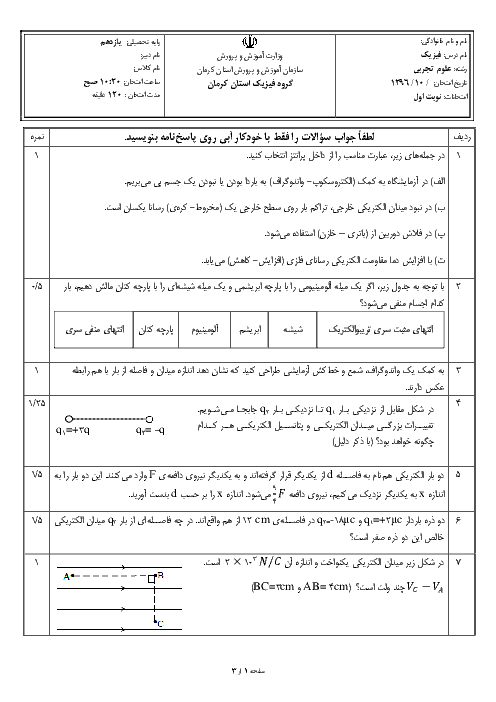
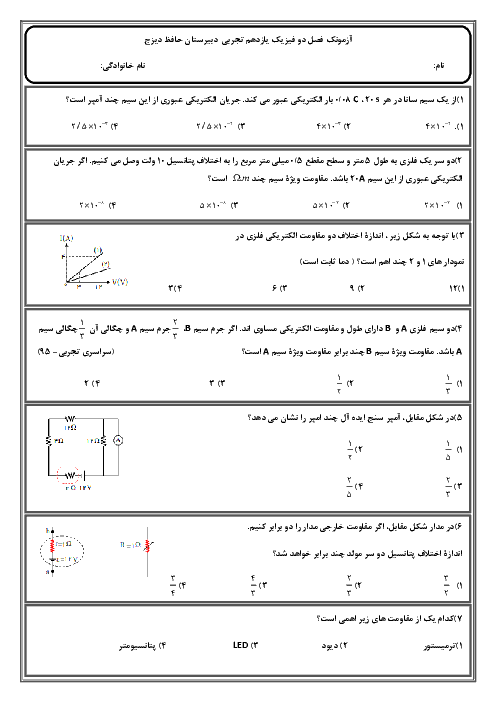
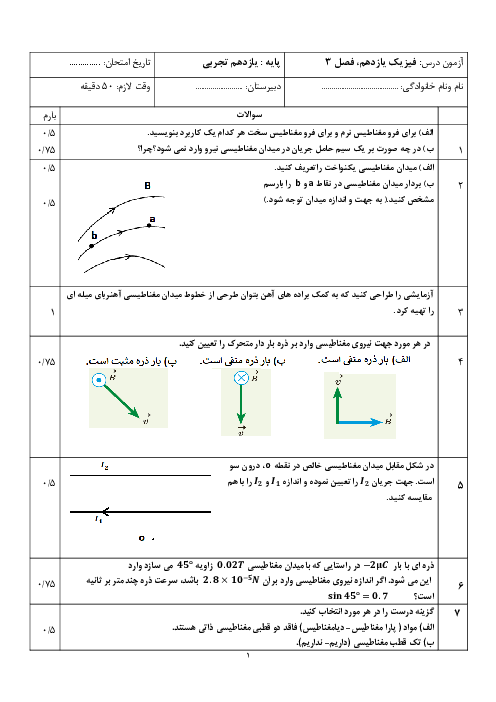
در حالت اول نیروهای وارد بر ${{q}_{2}}$ را مشخص کرده و مقدار آن‌ها را حساب می‌کنیم:

با توجه به تصویر

$\begin{align}  & {{F}_{12}}=k\frac{\left| {{q}_{1}} \right|\left| {{q}_{2}} \right|}{r_{12}^{2}}\Rightarrow {{F}_{12}}=k\frac{q\times 2q}{4{{d}^{2}}}=0/5k\frac{{{q}^{2}}}{{{d}^{2}}} \\  & {{F}_{32}}=k\frac{\left| {{q}_{2}} \right|\left| {{q}_{3}} \right|}{r_{32}^{2}}\Rightarrow {{F}_{32}}=k\frac{2q\times 2q}{{{d}^{2}}}=4k\frac{{{q}^{2}}}{{{d}^{2}}} \\ \end{align}$ 

با توجه به این‌که این دو نیرو در خلاف جهت یکدیگرند، برآیند آن‌ها برابر با $F=3/5k\frac{{{q}^{2}}}{{{d}^{2}}}$ می‌شود.

در حالت دوم و با توجه به تصویر دوم داریم:

$\begin{align}  & {{F}_{12}}=k\frac{\left| {{q}_{1}} \right|\left| {{q}_{2}} \right|}{{{r}^{2}}}\Rightarrow {{F}_{12}}=k\frac{q\times 2q}{{{d}^{2}}}=2k\frac{{{q}^{2}}}{{{d}^{2}}} \\  & {{F}_{32}}=k\frac{\left| {{q}_{2}} \right|\left| {{q}_{3}} \right|}{r_{32}^{2}}\Rightarrow {{F}_{32}}=k\frac{2q\times 3q}{{{d}^{2}}}=6k\frac{{{q}^{2}}}{{{d}^{2}}} \\ \end{align}$

با توجه به علامت بارها، این دو نیرو هم‌جهت بوده و برآیند آن‌ها ${F}'=8k\frac{{{q}^{2}}}{{{d}^{2}}}$ می‌شود.

در نتیجه نسبت اندازهٔ برآیند نیروهای وارد بر ${{q}_{2}}$ در حالت دوم به حالت اول برابر است با:

$\frac{{{F}'}}{F}=\frac{8k\frac{{{q}^{2}}}{{{d}^{2}}}}{3/5k\frac{{{q}^{2}}}{{{d}^{2}}}}=\frac{16}{7}$