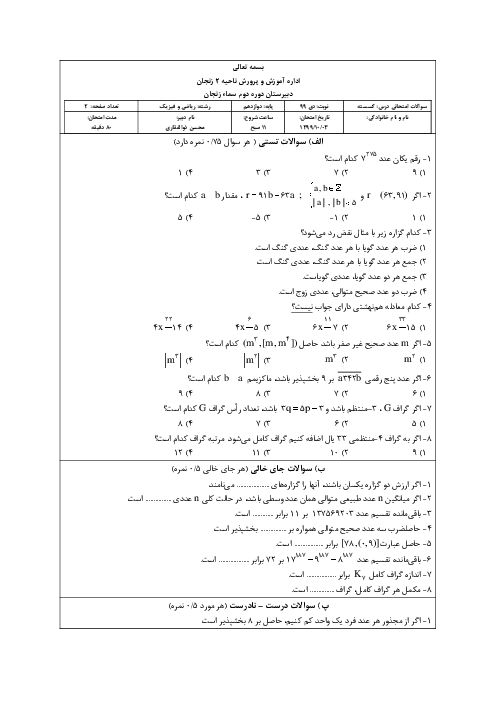
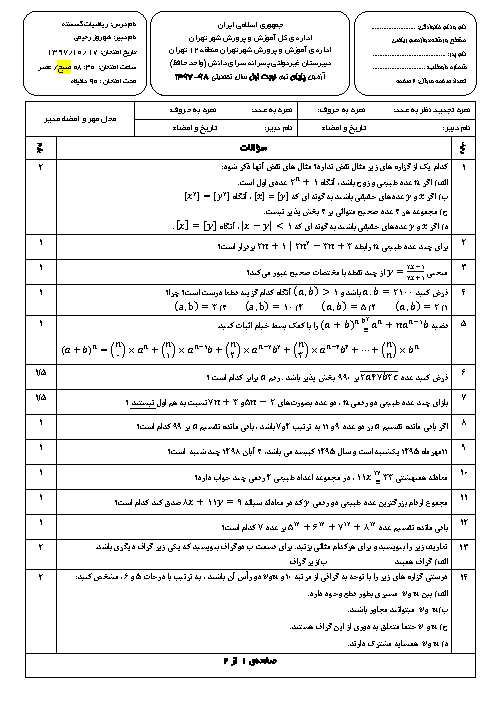
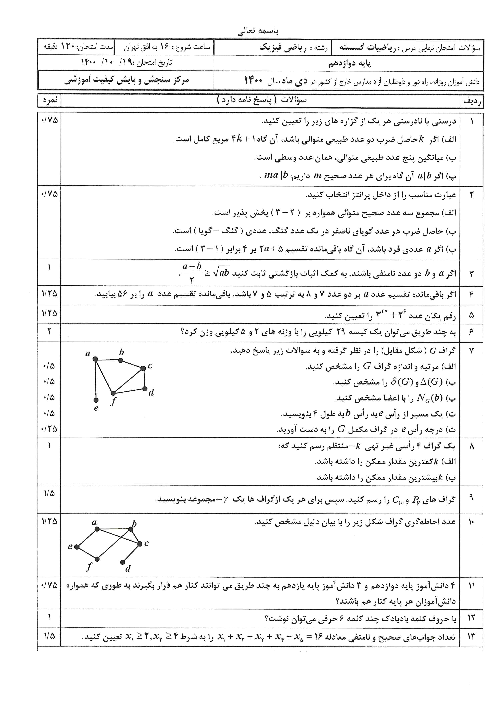
باید تعداد جواب‌های معادلهٔ سیالهٔ خطی $150x+250y=3700$ را در مجموعهٔ اعداد صحیح و نامنفی بیابیم (در واقع $x$ و $y$ نشان دهندهٔ تعداد تمبرهای 150 و 250 ریالی است). ابتدا معادله را به ساده‌ترین صورت ممکن درمی‌آوریم. می‌توانیم طرفین این معادله را بر 50 تقسیم کنیم و به معادلهٔ $3x+5y=74$ برسیم. یک جواب از این معادله را به صورت ذهنی به دست می‌آوریم، مثلا $x=8$ و $y=10$. از روی این جواب می‌توانیم همهٔ جواب‌های معادله را تعیین کنیم.

به صورت زیر

$\left\{ \begin{matrix}   x=8+5k  \\   y=10-3k  \\\end{matrix} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,k\in Z$

برای محاسبهٔ تعداد جواب‌های معادله در مجموعهٔ اعداد صحیح و نامنفی به صورت زیر عمل می‌کنیم:

$\left\{ \begin{matrix}   8+5k\ge 0  \\   10-3k\ge 0  \\\end{matrix} \right.\Rightarrow \left\{ \begin{matrix}   5k\ge -8  \\   3k\le 10  \\\end{matrix} \right.\Rightarrow \left\{ \begin{matrix}   k\ge -1  \\   k\le 3  \\\end{matrix} \right.\Rightarrow -1\le k\le 3$

در نتیجه پاسخ برابر 5 است.