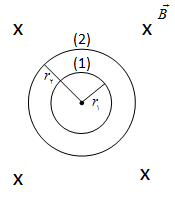مطابق شکل مقابل، دو حلقهٔ هممرکز $1$ و $2$ در میدان مغناطیسی درونسوی یکنواختی که بزرگی آن با آهنگ $2T/s$ تغییر میکند، قرار گرفتهاند. اگر شعاع حلقهٔ $2$ دو برابر شعاع حلقهٔ $1$ باشد، بزرگی نیروی محرکهٔ القا شده در حلقهٔ $2$ چند برابر بزرگی آن در حلقهٔ $1$ است؟