مقاومت يک رسانا از رابطهٔ مقابل به‌دست می‌آيد:   $R=\rho \frac{L}{A}$

در نتیجه برای محاسبهٔ تغییرات مقاومت داریم:

$\frac{{{R}_{1}}}{{{R}_{2}}}=\frac{{{\rho }_{2}}}{{{\rho }_{1}}}\times \frac{{{L}_{2}}}{{{L}_{1}}}\times \frac{{{A}_{1}}}{{{A}_{2}}}$   (1)

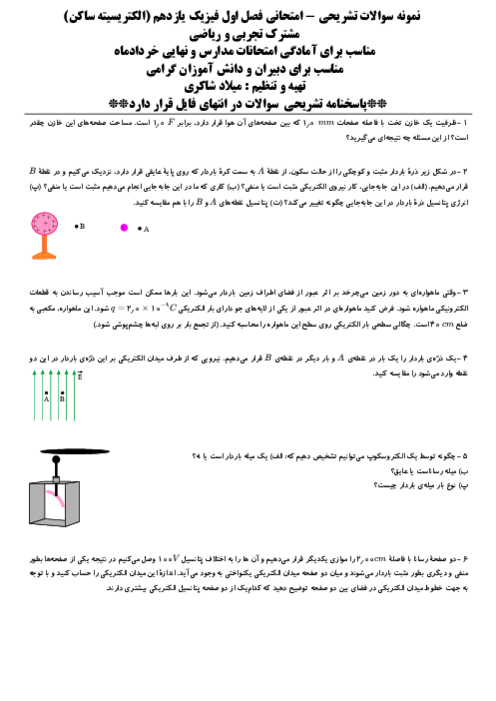
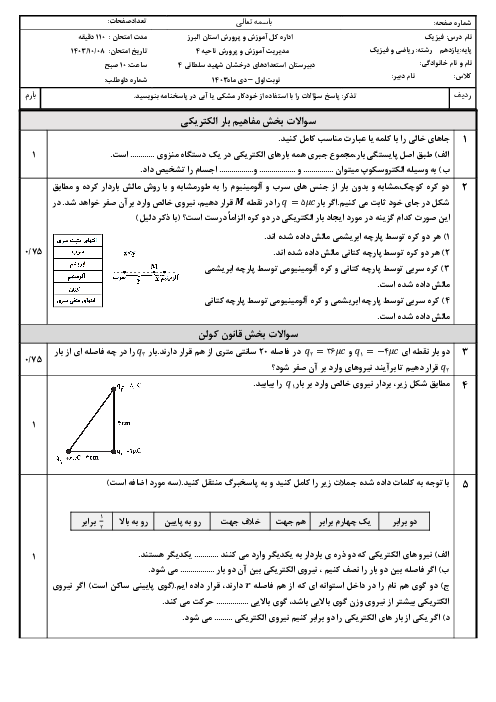
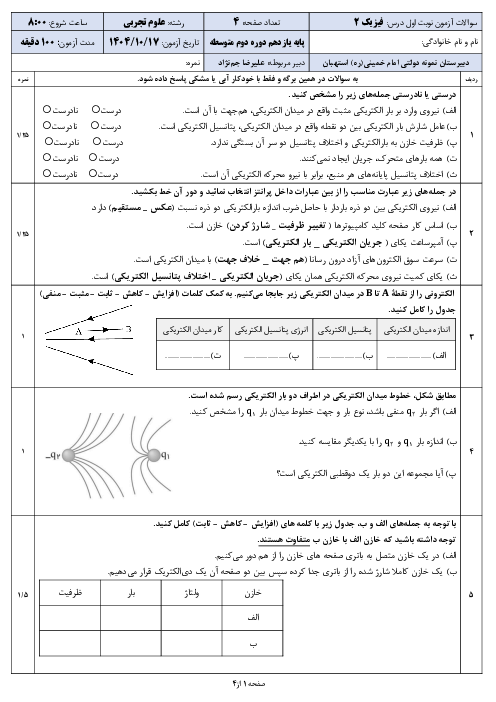
از آن جایی كه حجم مادهٔ استفاده شده ثابت است، تغییر سطح مقطع باعث تغییر طول می‌شود، در نتیجه خواهیم داشت:

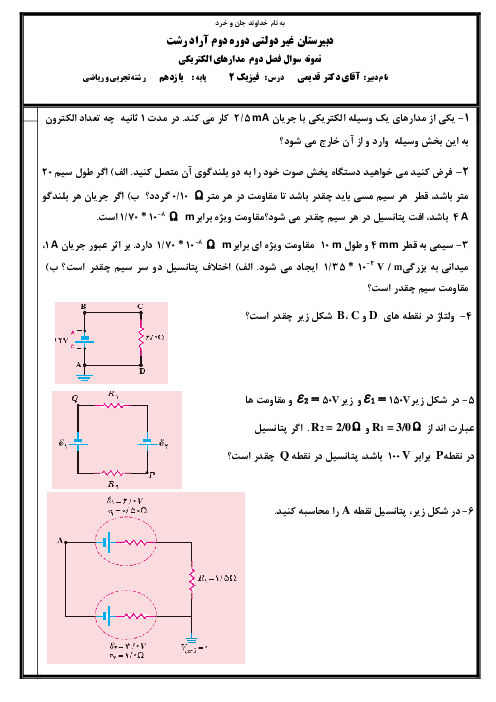
${{V}_{1}}={{V}_{2}}\Rightarrow {{L}_{1}}{{A}_{1}}={{L}_{2}}{{A}_{2}}\Rightarrow \frac{{{L}_{2}}}{{{L}_{1}}}=\frac{{{A}_{1}}}{{{A}_{2}}}$   (2)

$\xrightarrow[{{\rho }_{1}}={{\rho }_{2}}]{(2),(1)}\frac{{{R}_{2}}}{{{R}_{1}}}={{(\frac{{{A}_{1}}}{{{A}_{2}}})}^{2}}$

از آن جايی كه سطح مقطع متناسب است با توان دوم قطر، خواهيم داشت:

$\frac{{{R}_{2}}}{{{R}_{1}}}={{(\frac{{{D}_{1}}}{{{D}_{2}}})}^{4}}$

کاهش 36 درصدی مقاومت به این معنا است که ${{R}_{2}}={{R}_{1}}-\frac{36}{100}{{R}_{1}}=\frac{64}{100}{{R}_{1}}$ یعنی:

$\frac{{{R}_{2}}}{{{R}_{1}}}={{(\frac{{{D}_{1}}}{{{D}_{2}}})}^{4}}\Rightarrow \frac{64}{100}={{(\frac{{{D}_{1}}}{{{D}_{2}}})}^{4}}$

$\Rightarrow \frac{{{D}_{1}}}{{{D}_{2}}}=\frac{\sqrt{8}}{\sqrt{10}}=\frac{2\sqrt{2}}{\sqrt{10}}\Rightarrow \frac{{{D}_{2}}}{{{D}_{1}}}=\frac{\sqrt{10}}{2\sqrt{2}}=\frac{\sqrt{5}}{2}$