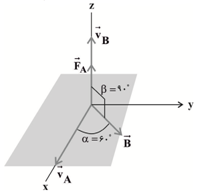
ذرهٔ $A$ با بار $۱۰\mu C$ و با تندی ۲۰ متر بر ثانيه در جهتی حركت می‌كند كه بردار سرعت آن با ميدان مغناطيسی يكنواخت زاويهٔ ۶۰ درجه می‌سازد. ذرهٔ $B$ با بار $۵nC$ عمود بر راستای حركت ذرهٔ $A$ و با تندی ۱۰ متر بر ثانيه به گونه‌ای حركت می‌كند كه بردار سرعت آن موازی بردار نيروی مغناطيسی وارد بر ذرهٔ $A$ است. بزرگی نيروی مغناطيسی وارد بر ذرهٔ $A$ چند برابر بزرگی نيروی مغناطيسی وارد بر ذرهٔ $B$ است؟