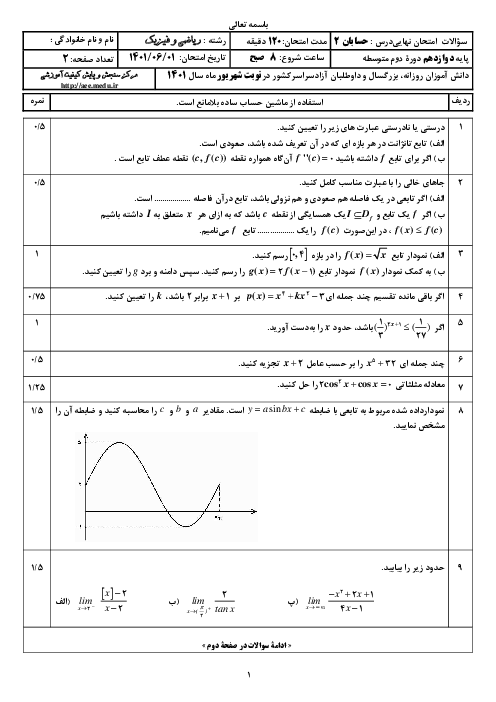
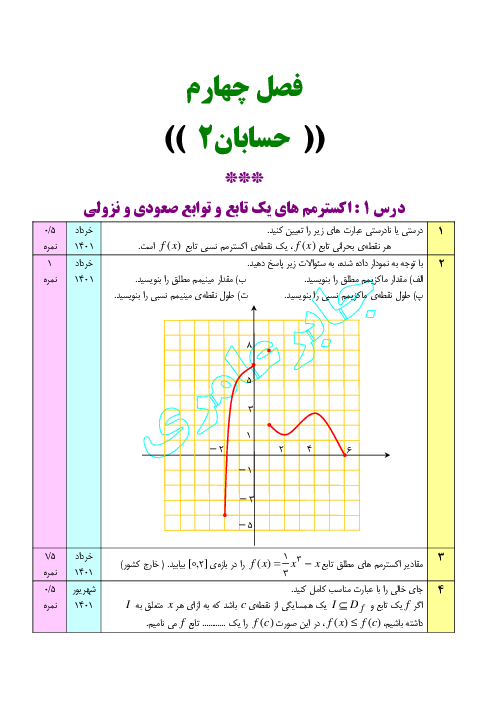
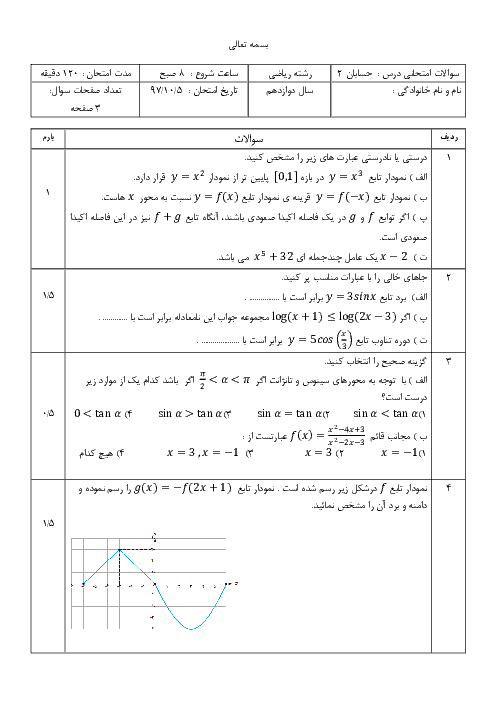
درس 2: مشتق پذیری و پیوستگی
حسابان (2)
دوازدهم
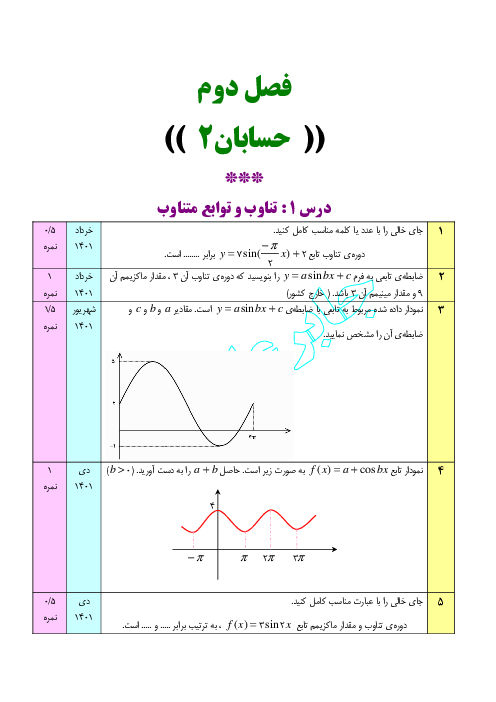
دوره دوم متوسطه- نظری
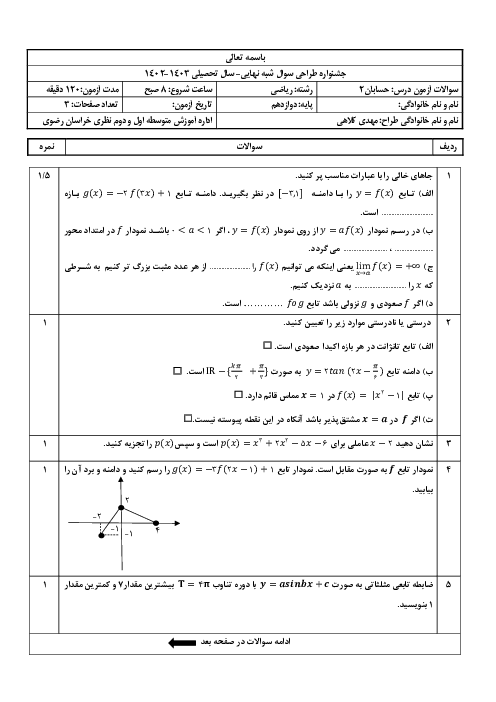
علوم ریاضی
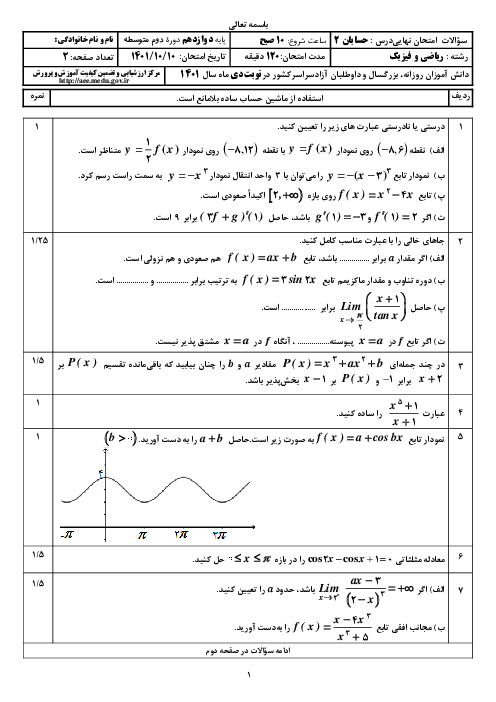
درسنامه آموزشی این مبحث
مشتق‌پذیری تابع $f(x) = \left\{ \begin{gathered}
{x^2} + 1\,\,\,\,\,\,x \geqslant 1 \hfill \\
3x - 1\,\,\,\,\,\,\,x \lt 1 \hfill \\
\end{gathered} \right.$ را در $x = 1$ بررسی کنید.
پاسخ تشریحی :
تحلیل ویدئویی تست
امیرحسین مزدور 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...