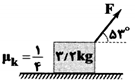
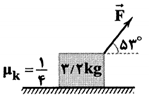
ابتدا برای محاسبه‌ی نیروی $\overrightarrow{F}$ باید $\sum{{{F}_{x}}}=0$ قرار داده و محاسبه را انجام دهیم، بنابراین:

$\sum{{{F}_{x}}}=0\Rightarrow F\cos {{53}^{{}^\circ }}-{{f}_{k}}=ma$

$\xrightarrow{{{f}_{k}}={{\mu }_{k}}N}F\cos {{53}^{{}^\circ }}-{{\mu }_{k}}N=ma$

$\xrightarrow{N=ma-F\sin {{53}^{{}^\circ }}}F\cos {{53}^{{}^\circ }}-{{\mu }_{k}}\left[ mg-F\sin {{53}^{{}^\circ }} \right]=ma$

$\xrightarrow[g=10\frac{N}{kg},\sin {{53}^{{}^\circ }}=0/8,a=0]{\cos {{53}^{{}^\circ }}=0/6,{{\mu }_{k}}=\frac{1}{4},m=3/2kg}0/6F-\frac{1}{4}\left[ 32-0/8F \right]=0$

$\Rightarrow 0/8F=8\Rightarrow F=10N$

با سه برابر شدن نیروی $\overrightarrow{F}$، این نیرو به $\overrightarrow{{{F}'}}=30N$ می‌رسد. حالا نیروی اصطکاک جنبشی را پس از 3 برابر شدن نیروی $\overrightarrow{F}$ به دست می‌آوریم:

در حالت دوم:

${{f}_{{{k}_{2}}}}={{\mu }_{k}}{{N}_{2}}={{\mu }_{k}}(mg-{F}'\sin {{53}^{{}^\circ }})\Rightarrow {{f}_{k}}=\frac{1}{4}(32-30(0/8)\Rightarrow {{f}_{{{k}_{2}}}}=2N$

در حالت اول:

${{f}_{{{k}_{1}}}}={{\mu }_{k}}{{N}_{1}}\Rightarrow {{f}_{{{k}_{1}}}}={{\mu }_{k}}(mg-{F}'\sin {{53}^{^{{}^\circ }}})\Rightarrow {{f}_{k}}=\frac{1}{4}(32-10(0/8)\Rightarrow {{f}_{{{k}_{1}}}}=6N$

پس نیروی اصطکاک $\frac{1}{3}$ برابر شده است.