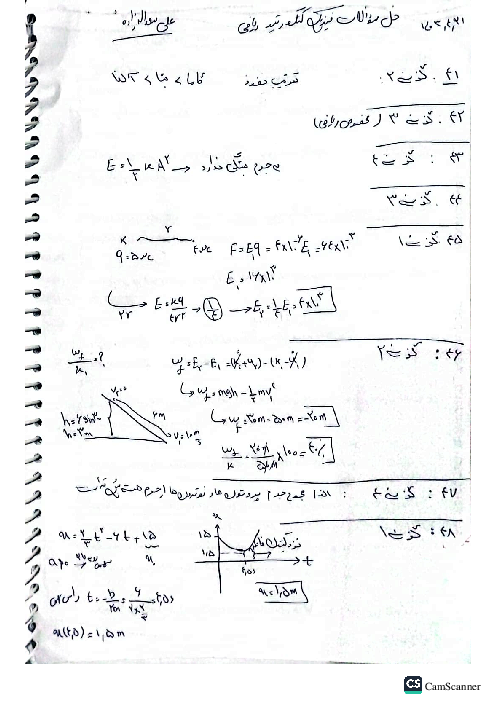
نوسانگری روی سطح افقی بدون اصطکاک نوسان میکند، لحظهای که جهت حرکت نوسانگر تغییر میکند، بزرگی شتاب آن $0/8{\pi ^2}\frac{m}{{{s^2}}}$ و لحظهای که نیروی وارد بر نوسانگر صفر میشود، بزرگی سرعت آن به $0/2\pi \frac{m}{s}$ میرسد. بزرگی شتاب نوسانگر در مکان $x = 1cm$ چند متر بر مربع ثانیه است؟