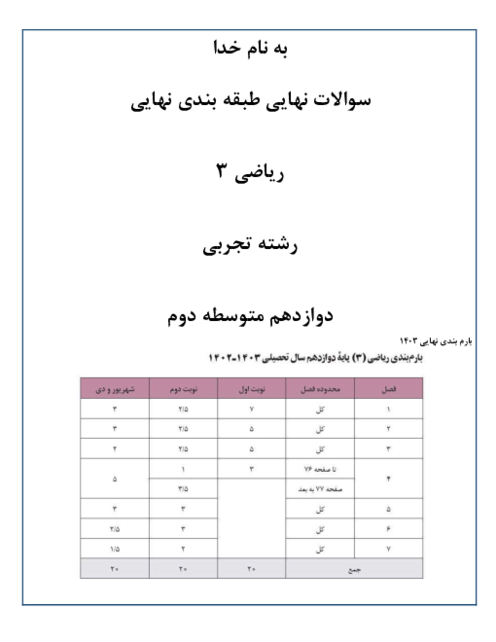
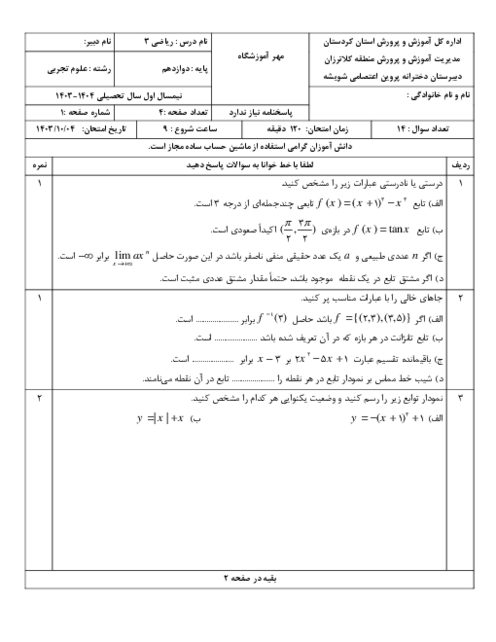
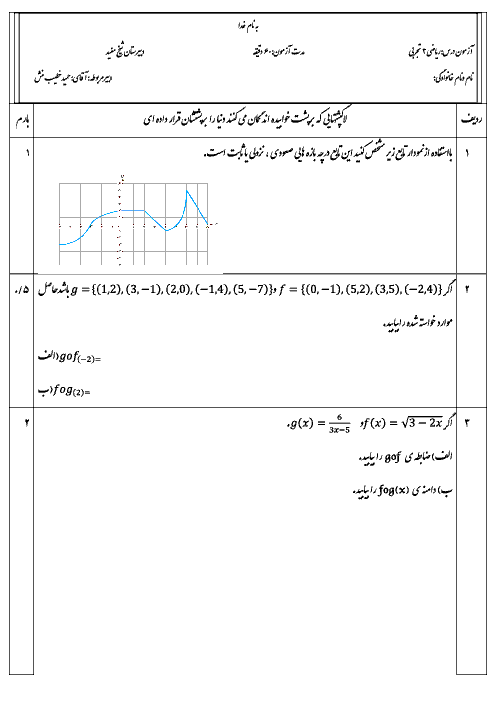
درس 1: توابع چند جمله‌ای- توابع صعودی و نزولی
ریاضی (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
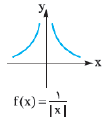
تابع $f(x)=\frac{1}{\left| x \right|}$ مفروض است. در کدام‌یک از بازه‌های زیر برای هر ${{x}_{1}}$ و ${{x}_{2}}$ عضو این بازه رابطهٔ ${{x}_{1}}<{{x}_{2}}\Leftrightarrow f({{x}_{1}})>f({{x}_{2}})$ برقرار است؟
تحلیل ویدئویی تست
علیرضا زینی وند 
مهدی خلجی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...