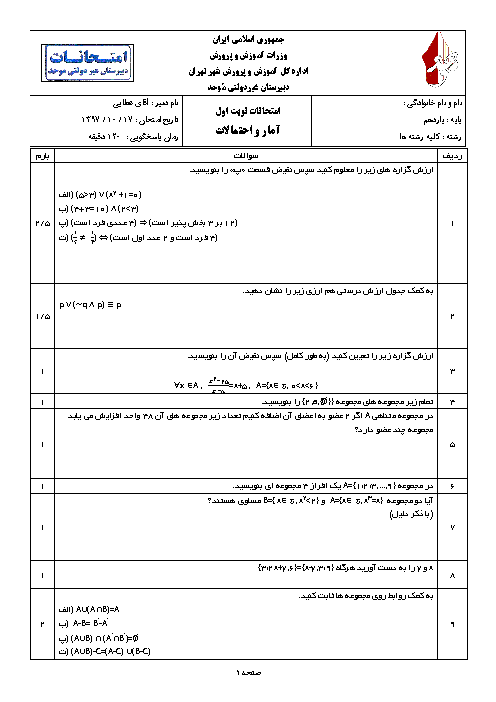
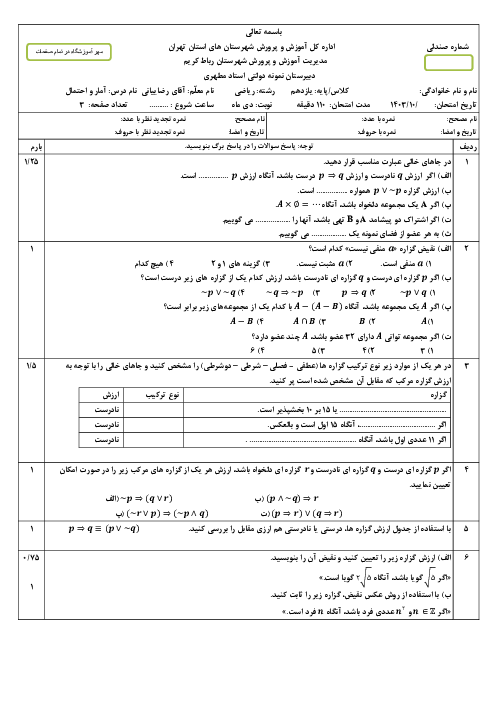
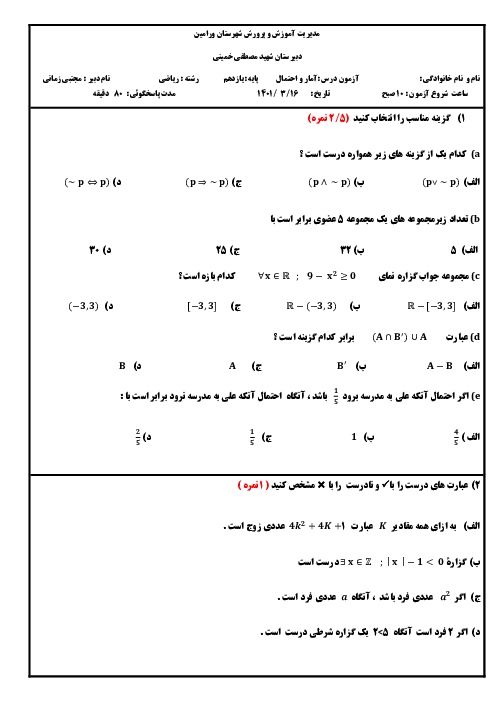
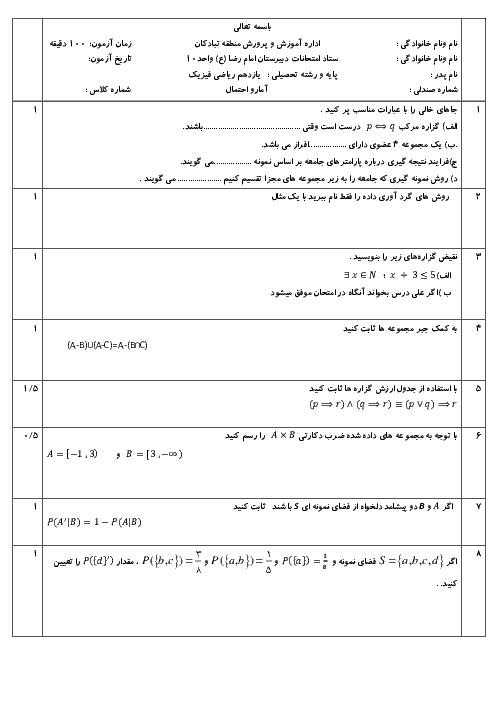
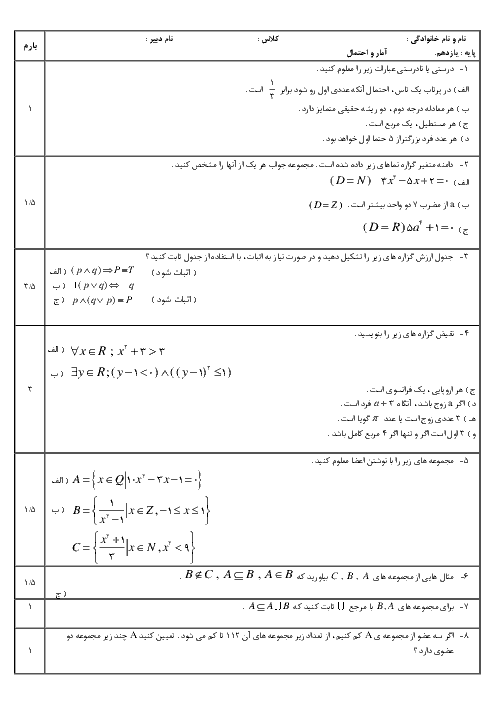
نكته‌ی 1: ميانگين و انحراف معيار n داده‌ی ${{x}_{1}}$، ${{x}_{2}}$، ${{x}_{3}}$، ... و ${{x}_{n}}$ به‌صورت زیر محاسبه می‌شوند:

میانگین $:\,\overline{X}=\frac{\sum\limits_{i=1}^{n}{{{X}_{i}}}}{n}$

انحراف معیار $:\,\sigma =\sqrt{\frac{\sum\limits_{i=1}^{n}{({{X}_{i}}-\overline{X})}}{n}}$

نکته‌ی 2: اگر نمونه‌ای تصادفی به‌اندازه‌ی N در اختیار داشته باشیم، با اطمینان بیش از 95 درصد می‌توانیم بگوییم:

$\overline{X}-\frac{2\sigma }{\sqrt{n}}\le \mu \le \overline{X}+\frac{2\sigma }{\sqrt{n}}$

که در آن $\mu $ میانگین جامعه، $\overline{X}$ میانگین نمونه و $\sigma $ انحراف معیار جامعه است.

نکته‌ی 3: خط فقر برابر است با نصف میانگین درآمد افراد جامعه.

$\overline{X}=\frac{7+6+6+5+4+3+2+2+1}{9}=\frac{36}{9}=4$

با توجه به نکته‌ی 1، ابتدا انحراف معیار داده‌ها را محاسبه می‌کنیم:

$\begin{align}
  & \sigma =\sqrt{\frac{{{(7-4)}^{2}}+2{{(6-4)}^{2}}+{{(5-4)}^{2}}+{{(4-4)}^{2}}+{{(3-4)}^{2}}+2{{(2-4)}^{2}}+{{(1-4)}^{2}}}{9}} \\ 
 & =\sqrt{\frac{36}{9}}=\sqrt{4}=2 \\ 
\end{align}$

حال با توجه به نکته‌ی 2، بازه‌ی اطمینان 95 درصدی را برای میانگین جامعه، حساب می‌کنیم:

$4-\frac{2\times 2}{\sqrt{9}}\le \mu \le 4+\frac{2\times 2}{\sqrt{9}}\Rightarrow 4-\frac{4}{3}\le \mu \le 4-\frac{4}{3}\Rightarrow \frac{8}{3}\le \mu \le \frac{16}{3}$

و در نهایت، با توجه به نکته‌ی 3 می‌دانیم که خط فقر، نصف میانگین جامعه است، پس:

$\frac{8}{\frac{3}{2}}\le Khate\,Faghr\le \frac{16}{\frac{3}{2}}\Rightarrow \frac{4}{3}\le Khate\,Faghr\le \frac{8}{3}$