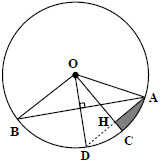
مطابق شکل زیر، در دایره‌ای به مساحت $\pi $، $A\hat OB = {120^ \circ }$ و $OH$ عمودمنصف $AD$ است. اختلاف محیط مثلث $AOH$ و محیط قسمت سایه زده شده کدام است؟
$\sqrt 3 - \frac{\pi }{6}$
2 )
$\sqrt 2 - \frac{\pi }{6}$
3 )
$\pi - \sqrt 3 $
4 )
$\pi - \sqrt 2 $
پاسخ تشریحی :
تحلیل ویدئویی تست
محسن ذوالفقاری 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...