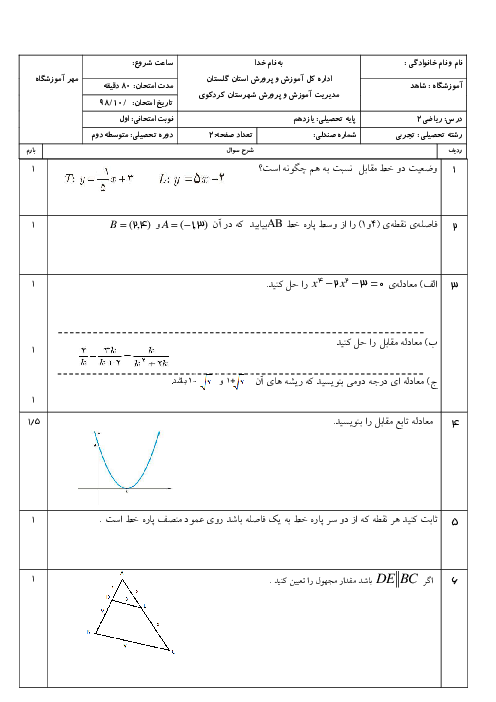
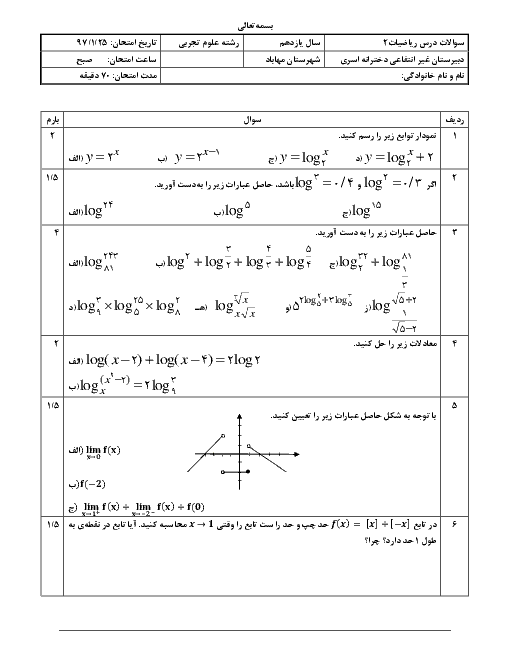
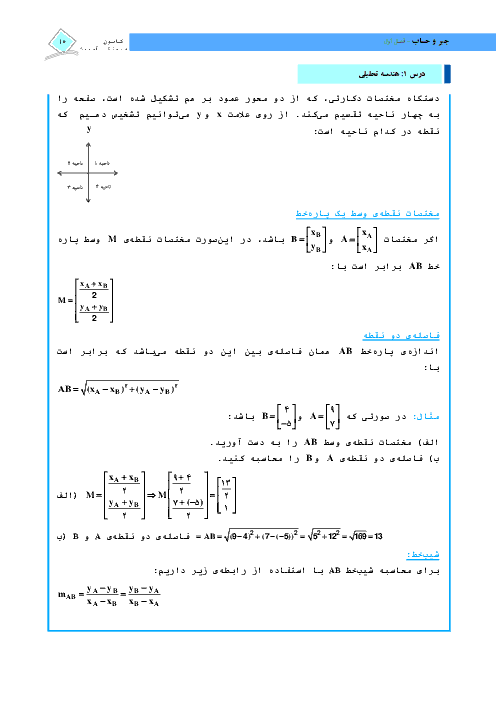
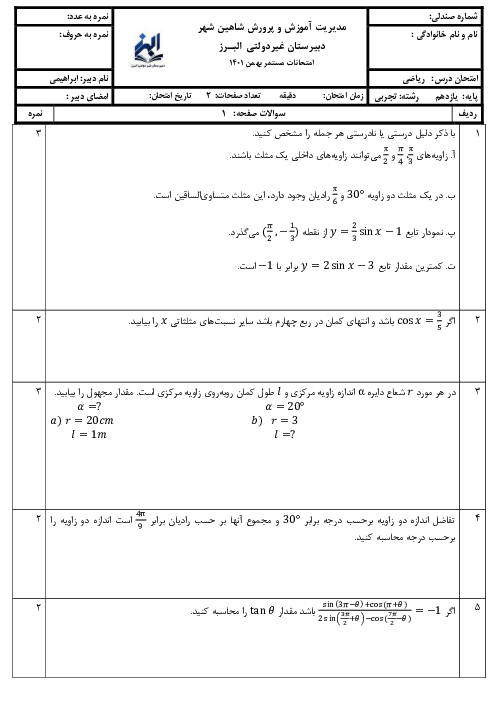
درس 3: معادلات گویا و معادلات رادیکالی
ریاضی (2)
یازدهم
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
دو نقطۀ A و B بر روی محور yها وجود دارد که فاصلۀ آنها از نقطۀ $P(3,2)$، برابر 5 است. حاصل ضرب عرضهای نقاط A و B چقدر است؟