اگر A و B دو پیشامد در فضای نمونه‌ای S باشند، به طوری که ، آنگاه احتمال وقوع پیشامد کدام است؟ | ریاضی (2) یازدهم شماره 64777 - گاما

گاما رو نصب کن!

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

گام به گام نوبت اول کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نمونه سوال تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم گزارش کارورزی

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

درس 1: احتمال شرطی و پیشامدهای مستقل ریاضی (2) یازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

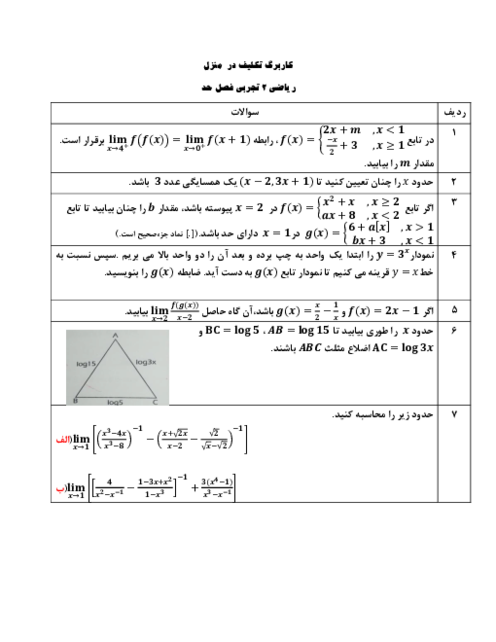
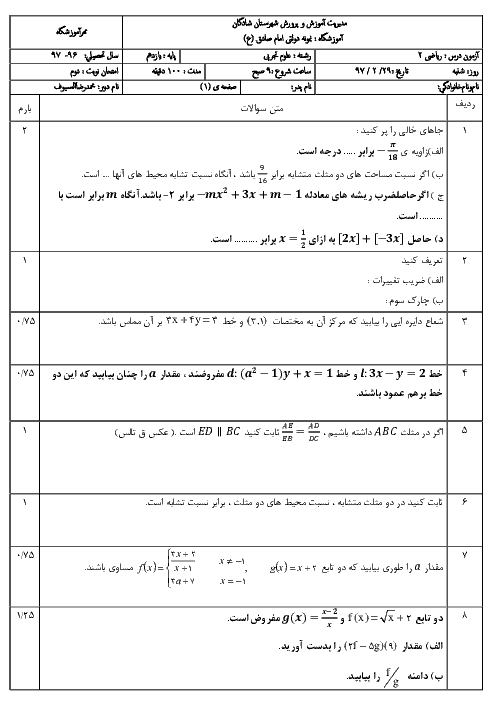
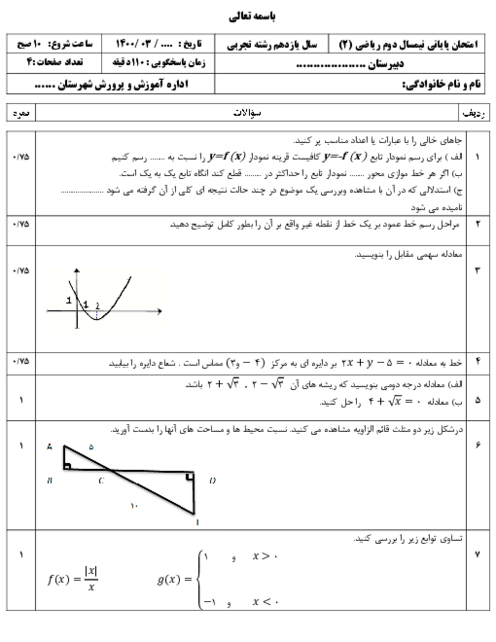
اگر A و B دو پیشامد در فضای نمونه‌ای S باشند، به طوری که $P(B)=0/3 , P(A|B')=0/4$، آنگاه احتمال وقوع پیشامد $A\cup B$کدام است؟

1 )

0/54

2 )

0/5

3 )

0/46

4 )

0/58

نمایش پاسخ

می‌دانیم $P( A - B)=P(A) - P(A \cap B) , A \cap B' = A - B $ هم‌چنین $P(B') = 1 - P(B)$ ، پس؛

$P(A | B') = \frac{P (A \cap B')}{ P(B')}= \frac{P(A - B)}{P(B')} \\ =\frac{P(A)-P(A \cap B)}{1-P(B)} (*) $

طبق فرض:

P(A | B')=0/4 , P(B) = 0/3

بنابراین از (*) نتیجه‌ می‌شود؛

$0/4 = \frac{P(A) - P(a \cap B)}{1 - 0/3} \Rightarrow P(A) - P(A \cap B) = 0/28 (**) $

از طرفی $ P(A \cup B) = P(A) + P(B) - P(A \cap B) = $ ، پس اگ به طفین تساوی (**) و $P(B)$ را اضافه کنیم، نتیجه می‌شود؛

$P(A) + P(B) - P(A \cap B) = 0/28 + P(B) \\ P(A \cup B) = 0/28 + 0/3 = 0/58 $

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

1403/04/23

عباس ابراهیمی علویجه

ویدیو دوره آموزشی، ریاضی (2) یازدهم دوره دوم متوسطه- نظری

مدرس: سیدطاها سیدعلی اللهی

مدت دوره: 17 ساعت (17 فایل)

با آلبوم تست، آزمون دلخواهتو بساز

سوپراستار

بسته ویژه نمره بیست: 5 نمونه سوال شبه نهایی ریاضی (2) یازدهم تجربی

23 صفحه

بسته ویژه نمره بیست: 5 نمونه سوال شبه نهایی ریاضی (2) یازدهم تجربی

ويژه نامه نوبت اول و…

سوپراستار

9 سری آزمون نوبت اول ریاضی (2) یازدهم تجربی دبیرستان سادات موسوی | دی 1399

18 صفحه

9 سری آزمون نوبت اول ریاضی (2) یازدهم تجربی دبیرستان سادات موسوی | دی…

داوود شهریاری

کتابچه آموزشی صفر تا صد کاملا مفهومی ریاضی یازدهم تجربی | فصل 1 الی 7

415 صفحه

کتابچه آموزشی صفر تا صد کاملا مفهومی ریاضی یازدهم تجربی | فصل 1 الی 7

سیدطاها سیدعلی اللهی

سوالات آزمون نوبت اول ریاضی (2) یازدهم دبیرستان دکتر بتول امام حسینی | دی 1400

4 صفحه

سوالات آزمون نوبت اول ریاضی (2) یازدهم دبیرستان دکتر بتول امام حسینی |…

نرگس نوفرد

رایـــــگان

سوالات امتحان ریاضی (2) پایه یازدهم رشتۀ تجربی دبیرستان پاسداران قزوین | فصل 1 و 2

2 صفحه

سوالات امتحان ریاضی (2) پایه یازدهم رشتۀ تجربی دبیرستان پاسداران قزوین…

حسن کلهر

آزمون پیوستگی ریاضی (2) یازدهم دبیرستان هفده شهریور

2 صفحه

آزمون پیوستگی ریاضی (2) یازدهم دبیرستان هفده شهریور

فریده نوروزی

امتحان نوبت دوم ریاضی یازدهم مدرسه غیردولتی دهخدا ناحیه 1 رشت | خرداد 1398

5 صفحه

امتحان نوبت دوم ریاضی یازدهم مدرسه غیردولتی دهخدا ناحیه 1 رشت | خرداد…

محمد پاک نژاد

آزمون نوبت اول ریاضی (2) یازدهم دبیرستان ایران دخت | دی 1399

2 صفحه

آزمون نوبت اول ریاضی (2) یازدهم دبیرستان ایران دخت | دی 1399

صدیقه کیان پور

امتحان میان ترم ریاضی (2) یازدهم دبیرستان حضرت معصومه اشکنان | ابتدای کتاب تا درس 1 از فصل سوم

4 صفحه

امتحان میان ترم ریاضی (2) یازدهم دبیرستان حضرت معصومه اشکنان | ابتدای…

سکینه باقری فرد

آزمون نوبت اول دیماه 1402 ریاضی2 یازدهم دبیرستان مشکات یزد

3 صفحه

آزمون نوبت اول دیماه 1402 ریاضی2 یازدهم دبیرستان مشکات یزد

نرگس نوفرد

موارد بیشتر

موارد بیشتر

ارسال فایل

مساحت ذوزنقه‌ٔ ABCD را محاسبه کنید.

مساحت مثلثی با سه راس (2.5)A و (3.0) B و (0.2)C چقدر است؟

بیشترین مساحت مستطیلی که در مثلث قائم الزاویه‌ای که معادله وترش 2y-x-8=0 می‌باشد محصور شده و یک راس مستطیل بر روی وتر مثلث قرار گرفته است چقدر است ؟

موارد بیشتر

ارسال پرسش

موارد بیشتر