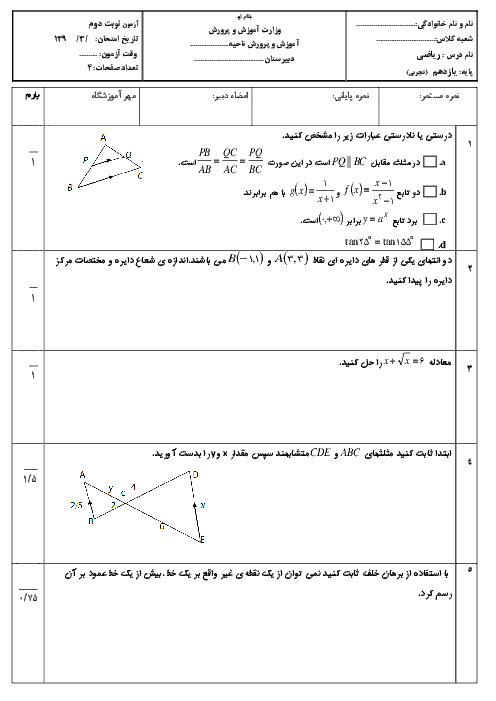
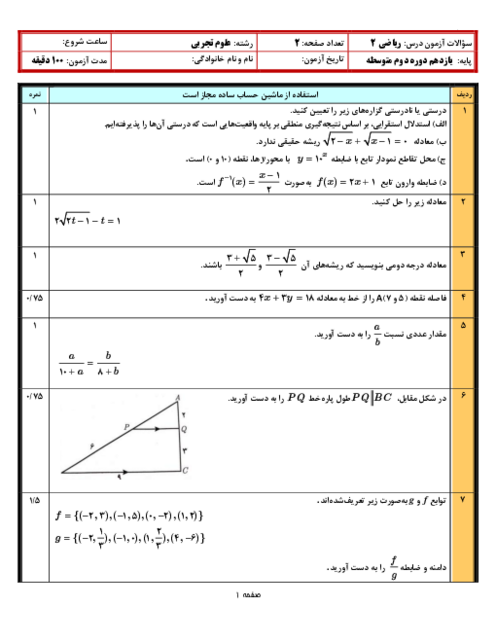
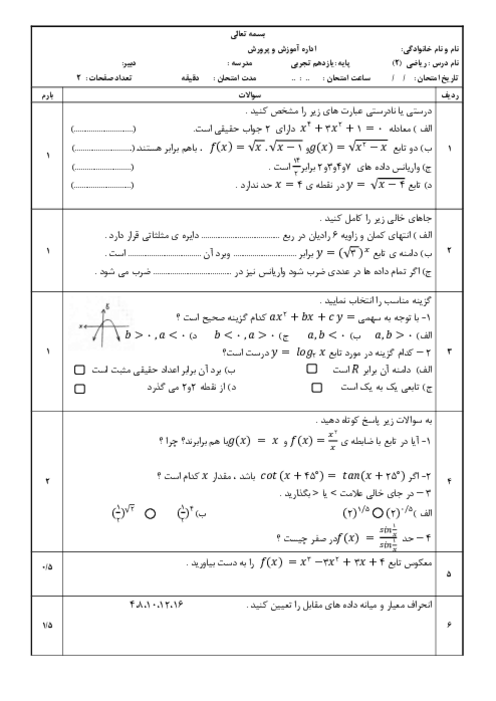
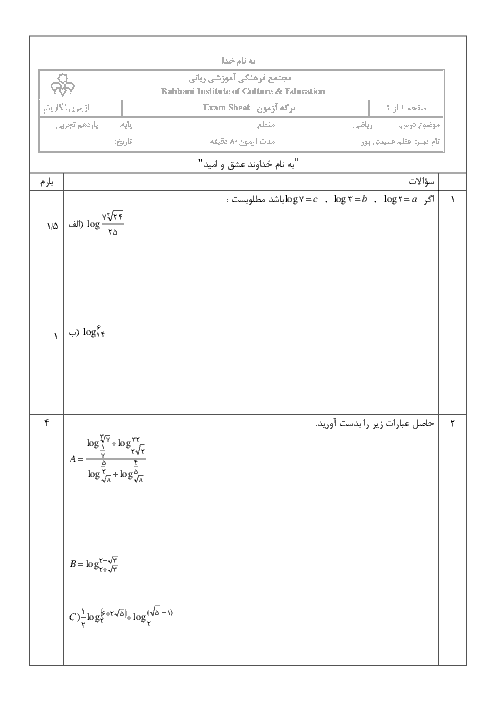
درس 2: معادلهٔ درجهٔ دوم و تابع درجه 2
ریاضی (2)
یازدهم
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
اگر محل تلاقی نمودار یک سهمی با محور xها، نقاطی به طولهای 1 و 2 باشد و سهمی محور عرضها را در نقطهای به عرض 4 قطع كند، طول رأس سهمی كدام است؟