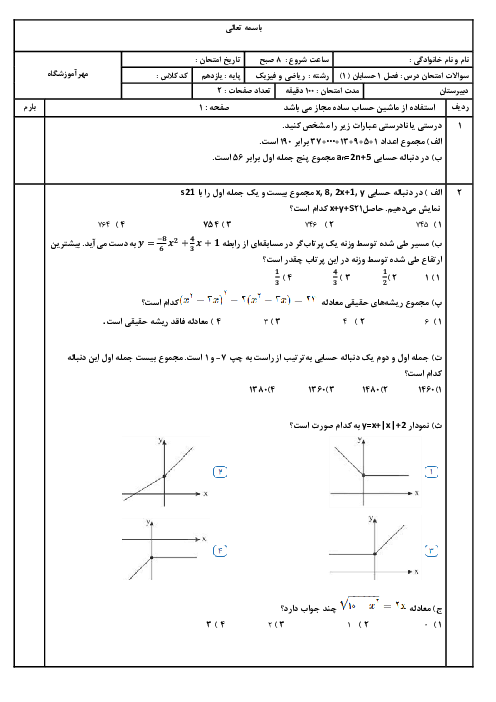
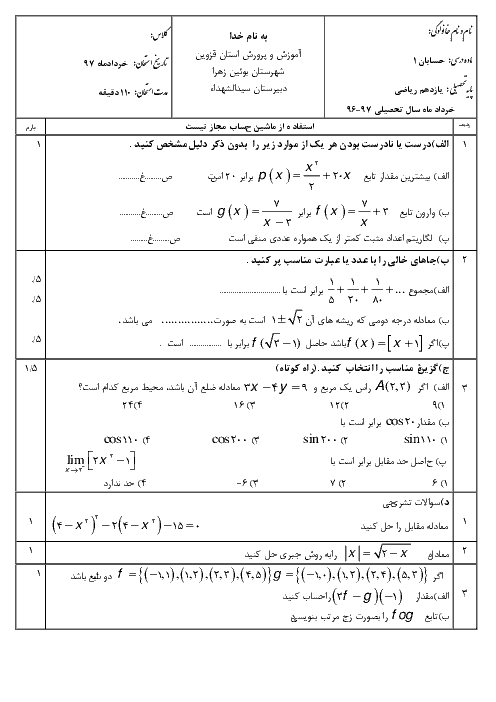
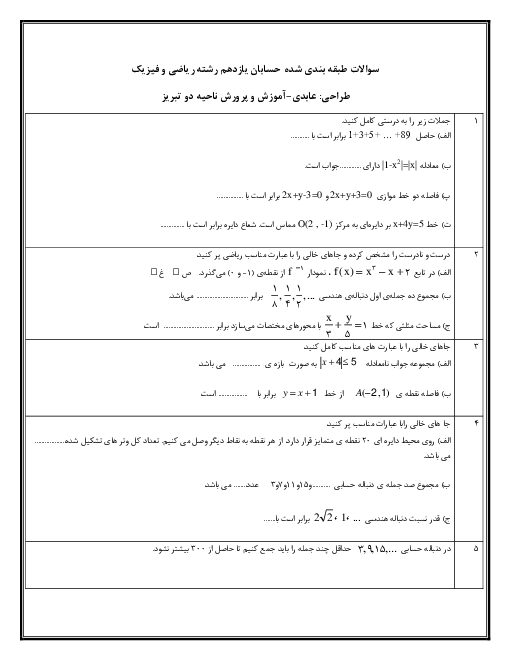
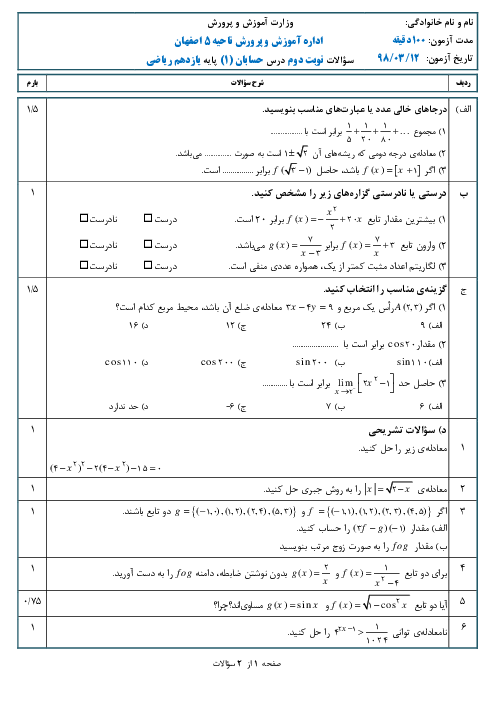
راه‌حل اول:

نکته: $Cot\alpha =\frac{\operatorname{Cos}\alpha }{\operatorname{Sin}\alpha },\operatorname{Sin}(\alpha -\beta )=\operatorname{Sin}\alpha \operatorname{Cos}\beta -\operatorname{Cos}\alpha \operatorname{Sin}\beta $

با استفاده از نكته می‌توان نوشت: 

$\operatorname{Sin}2\alpha Cot\alpha -\operatorname{Cos}2\alpha =\frac{\operatorname{Sin}2\alpha \operatorname{Cos}\alpha }{\operatorname{Sin}\alpha }-\operatorname{Cos}2\alpha =\frac{\operatorname{Sin}2\alpha \operatorname{Cos}\alpha -\operatorname{Cos}2\alpha \operatorname{Sin}\alpha }{\operatorname{Sin}\alpha }=\frac{\operatorname{Sin}(2\alpha -\alpha )}{\operatorname{Sin}\alpha }=\frac{\operatorname{Sin}\alpha }{\operatorname{Sin}\alpha }=1$

راه‌حل دوم:

نکته: $\operatorname{Sin}2\alpha =2\operatorname{Sin}\alpha \operatorname{Cos}\alpha ,\operatorname{Cos}2\alpha =2{{\operatorname{Cos}}^{2}}\alpha -1$

با توجه به نكته داريم: 

$\operatorname{Sin}2\alpha Cot\alpha -\operatorname{Cos}2\alpha =(2\operatorname{Sin}\alpha \operatorname{Cos}\alpha )(\frac{\operatorname{Cos}\alpha }{\operatorname{Sin}\alpha })-(2{{\operatorname{Cos}}^{2}}\alpha -2{{\operatorname{Cos}}^{2}}\alpha +1=1$