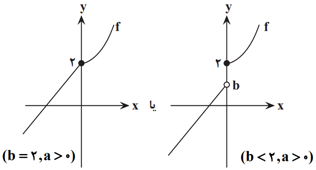
اگر تابع $f(x)=\left\{ \begin{matrix} \begin{matrix} {{x}^{2}}+2 & x\ge 0 \\ \end{matrix} \\ \begin{matrix} ax+b & x\lt 0 \\ \end{matrix} \\ \end{matrix} \right.$ يک به يک باشد، آنگاه حدود قابل قبول برای $a$ و $b$ كدام است؟
$\left\{ \begin{matrix} a\gt 0 \\ b\le 2 \\ \end{matrix} \right.$
2 )
$\left\{ \begin{matrix} a=1 \\ b\ge 2 \\ \end{matrix} \right.$
3 )
$\left\{ \begin{matrix} a\lt 0 \\ b\le 2 \\ \end{matrix} \right.$
4 )
$\left\{ \begin{matrix} a\gt 0 \\ b\ge 2 \\ \end{matrix} \right.$
پاسخ تشریحی :
تحلیل ویدئویی تست
مهدی خلجی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...