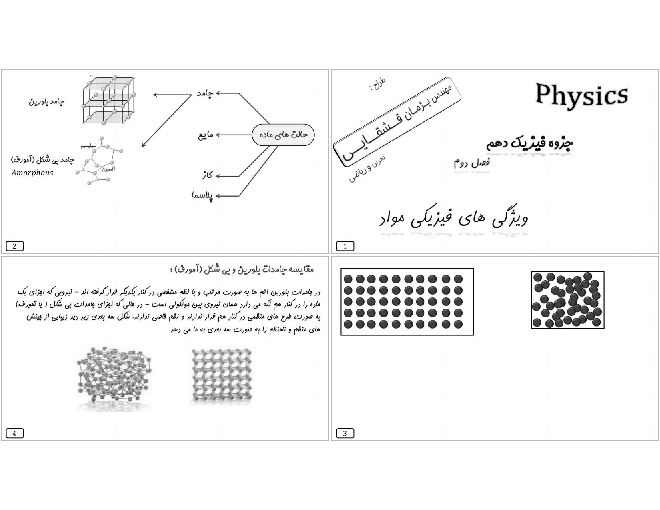
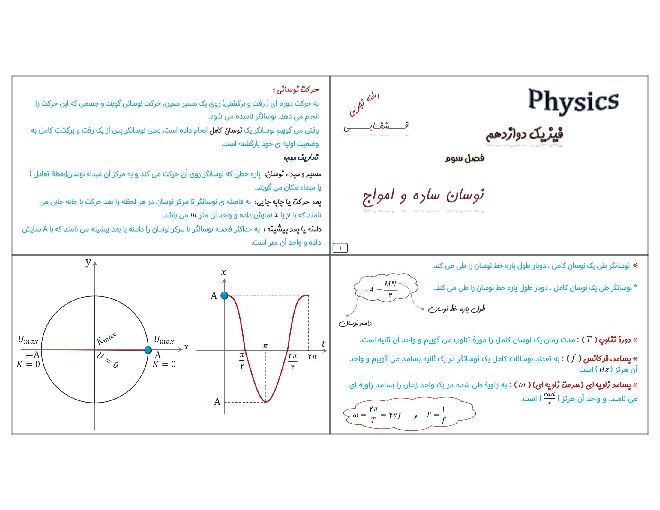
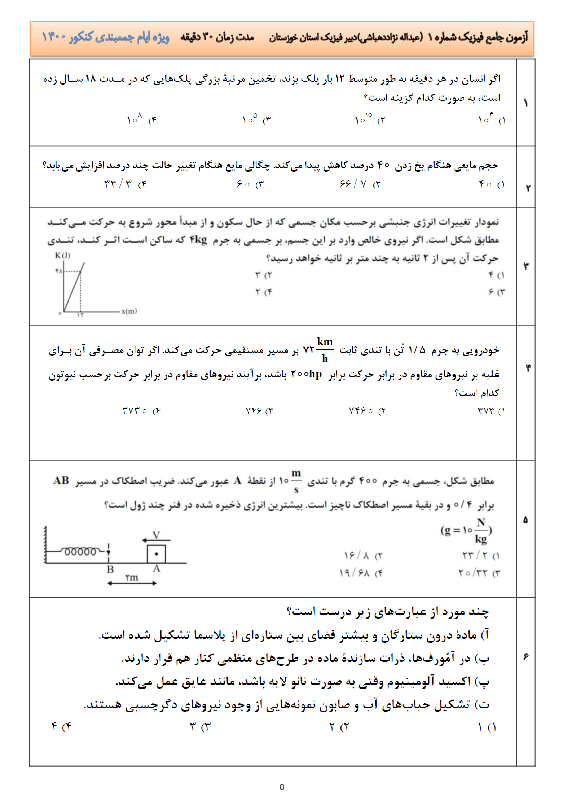
این تست را با یک تکنیک مفهومی به راحتی می‌شود پاسخ داد. اما ما ابتدا روشی را که احتمالاً زودتر به ذهن می‌رسد، می‌آوریم.
حالت اول: مطابق شکل (الف) و با توجه به اینکه سرعت متحرک در این حالت ثابت است، داریم:

${{F}_{net(y)}}=0\Rightarrow {{F}_{{{N}_{1}}}}-mg-{{F}_{2}}=0\Rightarrow {{F}_{{{N}_{1}}}}=mg+{{F}_{2}}=40+10=50N$

سرعت ثابت است $\Rightarrow {{F}_{net(x)}}=0\Rightarrow {{F}_{1}}-{{f}_{{{k}_{1}}}}=0\Rightarrow {{f}_{{{k}_{1}}}}={{F}_{1}}=10N$

حالت دوم: با توجه به شکل (ب) می‌توانیم ${{F}_{{{N}_{2}}}}$ را حساب کنیم:

${{F}_{{{N}_{2}}}}+{{F}_{2}}-mg=0\Rightarrow {{F}_{{{N}_{2}}}}+10-40=0\Rightarrow {{F}_{{{N}_{2}}}}=30N$

ضریب اصطکاک جنبشی در دو حالت برابر است و داریم:

${{\mu }_{k}}=\frac{{{f}_{k}}}{{{F}_{N}}}=$ مقدار ثابت $\Rightarrow \frac{{{f}_{{{k}_{1}}}}}{{{F}_{{{N}_{1}}}}}=\frac{{{f}_{{{k}_{2}}}}}{{{F}_{{{N}_{2}}}}}$

$\Rightarrow \frac{10}{50}=\frac{{{f}_{{{k}_{2}}}}}{30}\Rightarrow {{f}_{{{k}_{2}}}}=6N$

و اما پاسخ نهایی: در شکل‌های زیر نیرویی را که سطح بر جسم وارد می‌کند $(\overrightarrow{R})$، در دو حالت نشان داده‌ایم. طبق این شکل‌ها داریم:

$\left\{ \begin{matrix} \tan {{\theta }_{1}}=\frac{50}{10}=5 \\ \tan {{\theta }_{2}}=\frac{30}{6}=5 \\ \end{matrix} \right.\Rightarrow {{\theta }_{1}}={{\theta }_{2}}\lt {{90}^{{}^\circ }}$