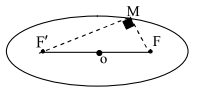
نقطه M روی بیضی به اقطار 6 و 10 واحد به گونه‌ای قرار دارد که فاصله آن تا مرکز بیضی برابر 4 واحد است. در صورتی که بدانیم مثلث $MFF'$ قائم الزاویه است، طول $MF$ را به دست آورید. ($F$ و $F'$ کانون‌های بیضی هستند.)
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...