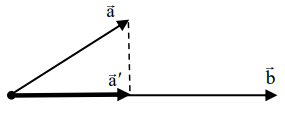
روش اول: بردار ${\vec a'}$ با بردار ${\vec b}$ موازی است،  $\vec a'\parallel \vec b \Rightarrow \vec a' = k\vec b$

$\eqalign{
  & (\vec a - \vec a') \bot \vec b \Rightarrow (\vec a - \vec a').\vec b = 0 \cr
  & \Rightarrow \vec a.\vec b - (k\vec b).\vec b = 0 \Rightarrow   \cr 
  & k = \frac{{\vec a.\vec b}}{{{{\left| {\vec b} \right|}^2}}} \cr
 & \Rightarrow \vec a' = k\vec b = \frac{{\vec a.\vec b}}{{{{\left| {\vec b} \right|}^2}}}\vec b \cr} $

روش دوم: در مثلث قائم‌الزاویه، زاویه بین دو بردار  ${\vec a}$ و ${\vec b}$ را $\theta $ می‌نامیم، $\cos \theta  = \frac{{\left| {\vec a'} \right|}}{{\left| {\vec a} \right|}} \Rightarrow \left| {\vec a'} \right| = \left| {\vec a} \right|\cos \theta $

$\eqalign{
  & \vec a' = k\vec b \Rightarrow \left| {\vec a'} \right| = k\left| {\vec b} \right|  \cr
 & \Rightarrow k = \frac{{\left| {\vec a'} \right|}}{{\left| {\vec b} \right|}} = \frac{{\left| {\vec a} \right|\cos \theta }}{{\left| {\vec b} \right|}} = \frac{{\left| {\vec b} \right|\left| {\vec a} \right|\cos \theta }}{{{{\left| {\vec b} \right|}^2}}} =   \cr 
  & \frac{{\vec a.\vec b}}{{{{\left| {\vec b} \right|}^2}}}\mathop  \to \limits^{\vec a' = k\vec b} \vec a' = \frac{{\vec a.\vec b}}{{{{\left| {\vec b} \right|}^2}}}\vec b \cr} $