در شکل مقابل، در لوله‌ی شکل مقدار جیوه در حال تعادل قرار دارد. اگر قطر سمت چپ لوله نصف قطر راست آن باشد و به ارتفاع از مایعی به چگالی در سمت چپ روی جیوه بریزیم،…

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

** فصل 2: ویژگی‌های فیزیکی مواد فیزیک (1) دهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

در شکل مقابل، در لوله‌ی $U$ شکل مقدار جیوه در حال تعادل قرار دارد. اگر قطر سمت چپ لوله نصف قطر راست آن باشد و به ارتفاع $5cm$ از مایعی به چگالی $3/4\frac{g}{c{{m}^{3}}}$ در سمت چپ روی جیوه بریزیم، جیوه در سمت راست چند سانتی‌متر از محل کنونی بالاتر می‌رود؟ $({{\rho }_{Hg}}=13/6\frac{g}{c{{m}^{3}}})$

1 )

$0/25$

2 )

$1$

3 )

$4$

4 )

$\frac{3}{4}$

نمایش پاسخ

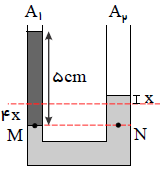
وقتی مایع را روی جیوه در سمت چپ می‌ریزیم جیوه در سمت چپ با اندازه‌ی ${{h}_{1}}$ پایین رفته و در سمت راست به اندازه‌ی ${{h}_{2}}$ بالا می‌رود. از آن‌جایی که قطر مقطع راست لوله دو برابر سمت چپ است. پس مساحت سمت راست $4$ برابر سمت چپ است، از سوی دیگر حجم مایع جابه‌جا شده در دو لوله برابر است، بنابراین داریم:

${{V}_{1}}={{V}_{2}}$

${{A}_{1}}{{h}_{1}}={{A}_{2}}{{h}_{2}}\Rightarrow {{h}_{2}}=\frac{1}{4}{{h}_{1}}\Rightarrow {{h}_{2}}=x\,\,,\,\,{{h}_{1}}=4x$

پس اختلاف ارتفاع جیوه در دو طرف لوله $5x$ است، پس اکنون با توجه به یکسان بودن فشار در نقاط هم‌تراز درون یک شاره ساکن، مانند نقاط $M$ و $N$ می‌توان نوشت:

${{P}_{M}}={{P}_{N}}\Rightarrow {{P}_{{}^\circ }}+{{(\rho gh)}_{Jiveh}}\Rightarrow {{(\rho h)}_{Maye}}={{(\rho h)}_{Jiveh}}\Rightarrow 3/4\times 5=13/6\times (5x)\Rightarrow 1=4x\Rightarrow x=0/25cm$