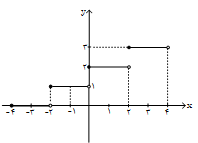
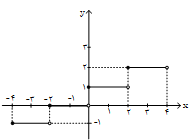
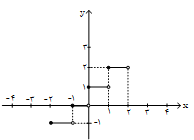
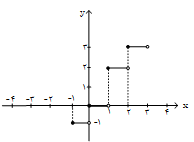
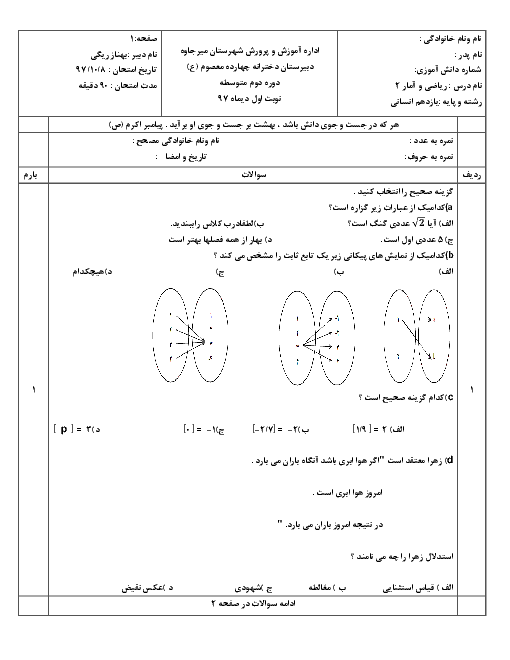
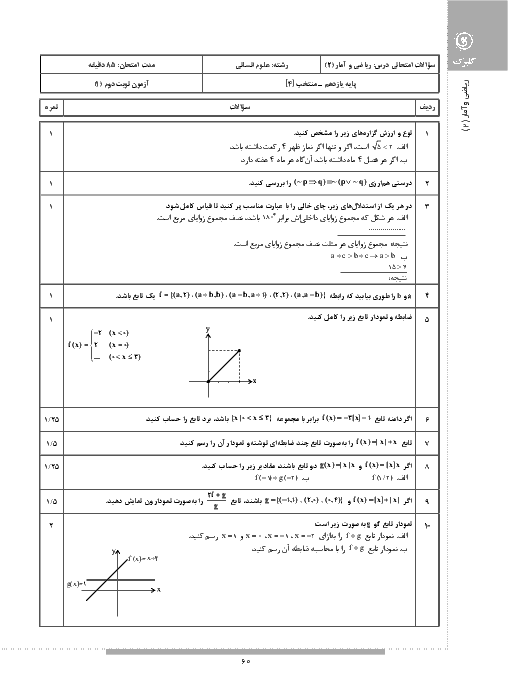
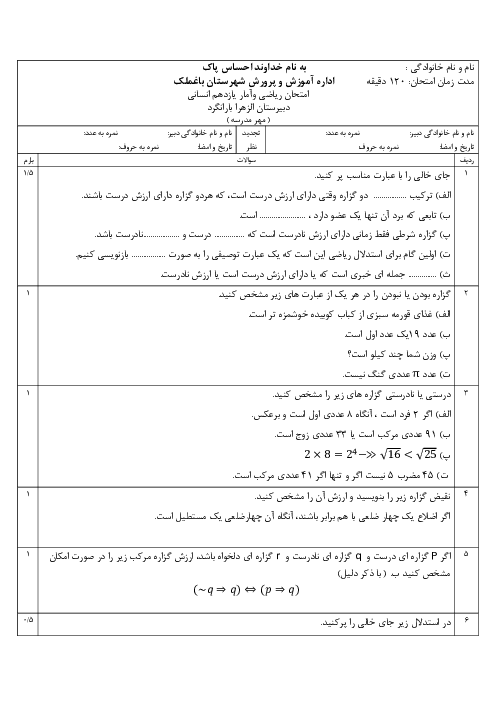
به‌ازای بازه‌های مختلف $x$، مقدار تابع را به‌دست می‌آوريم: 

$-2\le x\lt -1\Rightarrow -\frac{2}{2}\le \frac{x}{2}\lt -\frac{1}{2}\Rightarrow -1\le \frac{x}{2}\lt -\frac{1}{2}\Rightarrow -1+2\le \frac{x}{2}+2\lt \frac{-1}{2}+2$

$1\le \frac{x}{2}+2\lt \frac{3}{2}\Rightarrow \left[ \frac{x}{2}+2 \right]=1$

$-1\le x\lt 0\Rightarrow -\frac{1}{2}\le \frac{x}{2}\lt 0\Rightarrow -\frac{1}{2}+2\le \frac{x}{2}+2\lt 0+2\Rightarrow \frac{3}{2}\le \frac{x}{2}+2\lt 2$

$\Rightarrow \left[ \frac{x}{2}+2 \right]=1$

$0\le x\lt 1\Rightarrow 0\le \frac{x}{2}\lt \frac{1}{2}\Rightarrow 0+2\le \frac{x}{2}+2\lt \frac{1}{2}+2\Rightarrow 2\le \frac{x}{2}+2\lt \frac{5}{2}$

$\Rightarrow \left[ \frac{x}{2}+2 \right]=2$

$1\le x\lt 2\Rightarrow \frac{1}{2}\le \frac{x}{2}\lt \frac{2}{2}\Rightarrow \frac{1}{2}+2\le \frac{x}{2}+2\lt 1+2\Rightarrow \frac{5}{2}\le \frac{x}{2}+2\lt 3$

$\Rightarrow \left[ \frac{x}{2}+2 \right]=2$

$2\le x\lt 3\Rightarrow \frac{2}{2}\le \frac{x}{2}\lt \frac{3}{2}\Rightarrow 1+2\le \frac{x}{2}+2\lt \frac{3}{2}+2\Rightarrow 3\le \frac{x}{2}+2\lt \frac{7}{2}$

$\Rightarrow \left[ \frac{x}{2}+2 \right]=3$

$3\le x\lt 4\Rightarrow \frac{3}{2}\le \frac{x}{2}\lt \frac{4}{2}\Rightarrow \frac{3}{2}+2\le \frac{x}{2}+2\lt 2+2\Rightarrow \frac{7}{2}\le x+2\lt 4$

$\Rightarrow \left[ \frac{x}{2}+2 \right]=3$

با توجه به مقادير به‌دست آمده نتيجه می‌گيريم نمودار رسم شده در گزينه‌ی «1» صحيح است.