کوچک‌ترین ضریب تغییرات دسته‌های سه‌تایی از اعداد زوج متوالی دو رقمی با رقم دهگان یکسان، کدام است؟

گاما رو نصب کن!

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

گام به گام نوبت اول کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نمونه سوال تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم گزارش کارورزی

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

آمار ریاضی کنکور سراسری دوره دوم متوسطه- نظری علوم تجربی

کوچک‌ترین ضریب تغییرات دسته‌های سه‌تایی از اعداد زوج متوالی دو رقمی با رقم دهگان یکسان، کدام است؟

1 )

$3\sqrt {\frac{2}{3}} $

2 )

$\frac{1}{3}\sqrt {\frac{2}{3}} $

3 )

$\frac{1}{{12\sqrt 6 }}$

4 )

$\frac{1}{{24\sqrt 6 }}$

نمایش پاسخ

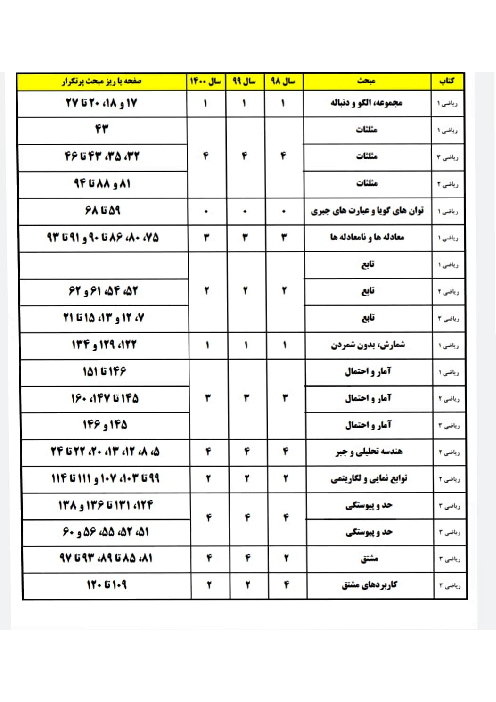
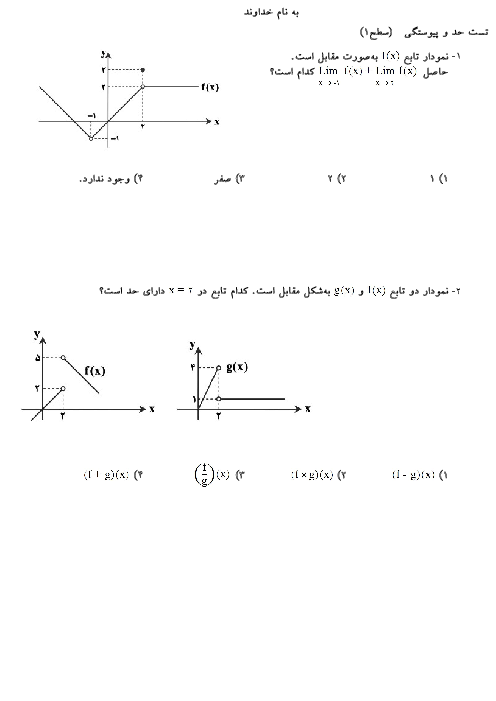
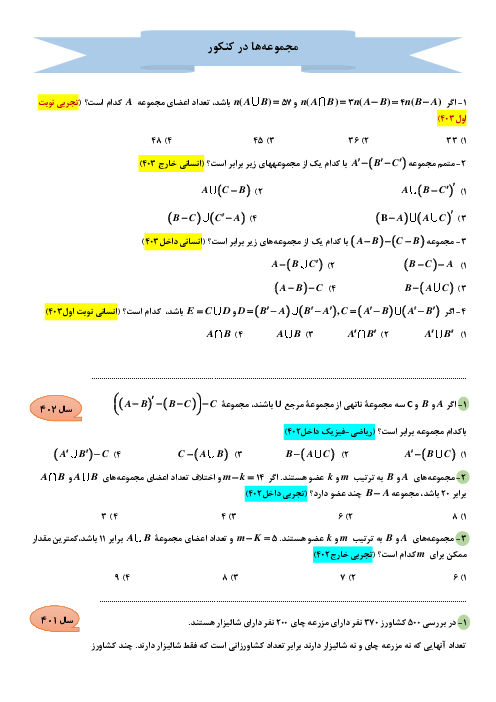
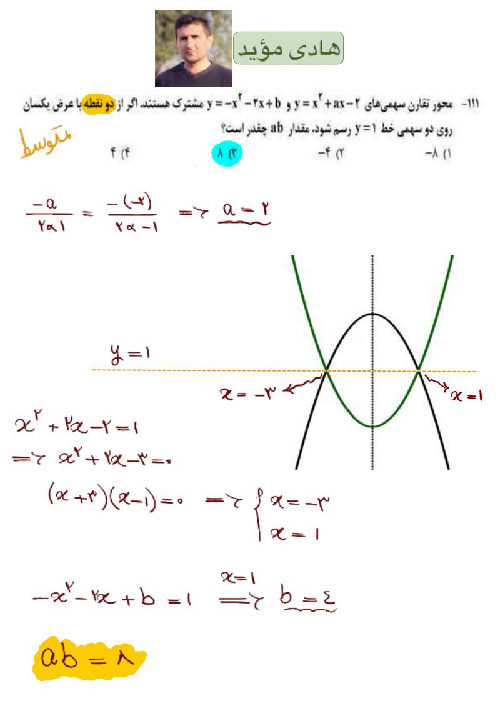
$\begin{array}{*{20}{c}}
x&{x + 2}&{x - 2 \to \bar x}
\end{array} = x + 2 \Rightarrow {\sigma ^2} = \frac{{{{( - 2)}^2} + 0 + {2^2}}}{3} = \frac{8}{3} \to \sigma = \sqrt {\frac{8}{3}} $

$CV = \frac{{\sqrt {\frac{8}{3}} }}{{\bar x}}$

از آنجا که ضریب تغییرات حداقل باید باشد، $\bar x$ باید بیشترین مقدار باشد. یعنی اعداد زوج به صورت 98، 96، 94 و $\bar x = 96$.

$CV = \frac{{2\frac{{\sqrt 2 }}{{\sqrt 3 }}}}{{96}} = \frac{{2\sqrt 2 }}{{96\sqrt 3 }} = \frac{{\sqrt 2 }}{{48\sqrt 3 }} \Rightarrow \frac{{\sqrt 2 }}{{48\sqrt 3 }} \times \frac{{\sqrt 2 }}{{\sqrt 2 }} = \frac{2}{{48\sqrt 6 }} = \frac{1}{{24\sqrt 6 }}$

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده