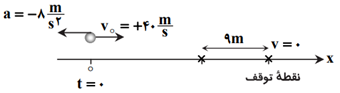
متحركی با شتاب ثابتی با اندازهٔ $۸\frac{m}{{{s}^{۲}}}$ روی خط راست حركت می‌كند. در لحظۀ $t=۰$ تندی آن $۴۰\frac{m}{s}$ و حركت متحرک كُندشونده است. در كدام لحظه برحسب ثانيه فاصلۀ متحرک تا نقطۀ توقف آن به ۹ متر می‌رسد؟