شش ضلعی منتظم به طول ضلع 2 واحد و نقطهٔ دلخواه درون آن مفروض‌اند. اگر نقطهٔ را به تمامی رئوس شش‌ضلعی وصل كنيم، آن‌گاه مجموع مساحت مثلث‌های ، و كدام است؟

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

درس 3: چند ضلعی‌های محاطی و محیطی هندسه (2) یازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

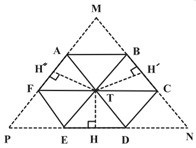
شش ضلعی منتظم $ABCDEF$ به طول ضلع 2 واحد و نقطهٔ دلخواه $T$ درون آن مفروض‌اند. اگر نقطهٔ $T$ را به تمامی رئوس شش‌ضلعی وصل كنيم، آن‌گاه مجموع مساحت مثلث‌های $TBC$، $TDE$ و $TAF$ كدام است؟

1 )

2 )

$4\sqrt{3}$

3 )

$3\sqrt{3}$

4 )

نمایش پاسخ

با امتداد دادن اضلاع شش‌ضلعی، مطابق شكل مثلث متساوی‌الاضلاع $MNP$ به طول ضلع 6 حاصل می‌شود.

از نقطهٔ $T$، عمودهای $TH$، $T{H}'$ و $T{H}''$ را به‌ترتيب بر اضلاع $DE$، $BC$ و $AF$ رسم می‌كنيم.

از طرفی می‌دانيم در يک مثلث متساوی‌الاضلاع، مجموع فواصل نقطه‌ای دلخواه درون آن تا اضلاع مثلث برابر با ارتفاع مثلث می‌باشد. بنابراين:

$TH+T{H}'+T{H}''=\frac{\sqrt{3}}{2}\times (6)=3\sqrt{3}$ (*)

حال به محاسبهٔ مجموع مساحت مثلث‌های مطلوب می‌پردازيم:

${{S}_{\underset{TBC}{\mathop{\Delta }}\,}}+{{S}_{\underset{TAF}{\mathop{\Delta }}\,}}+{{S}_{\underset{TDE}{\mathop{\Delta }}\,}}=\frac{1}{2}\times 2\times (TH+T{H}'+T{H}'')$

$\xrightarrow{(*)}{{S}_{\underset{TBC}{\mathop{\Delta }}\,}}+{{S}_{\underset{TAF}{\mathop{\Delta }}\,}}+{{S}_{\underset{TDE}{\mathop{\Delta }}\,}}=3\sqrt{3}$