پودمان 1: کاربرد برخی تابع‌ها در زندگی روزمره
ریاضی3 فنی
دوازدهم
دوره دوم متوسطه- فنی
الکترونیک (صنعت)
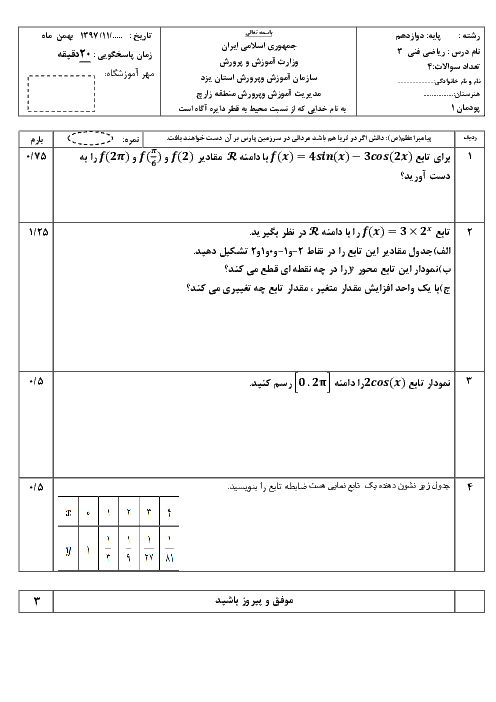
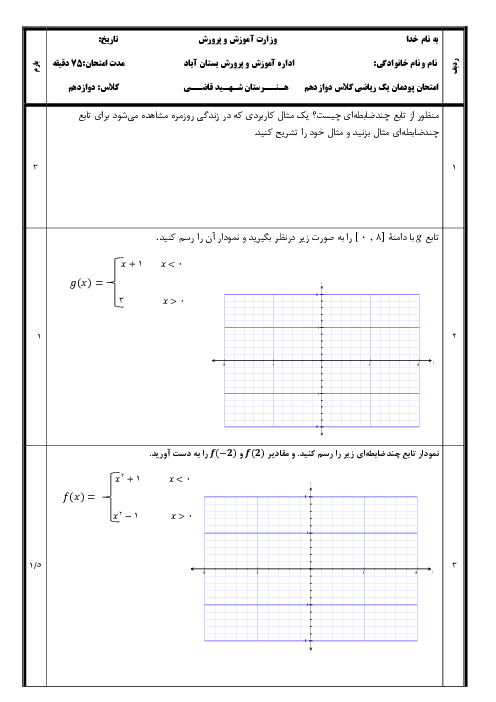
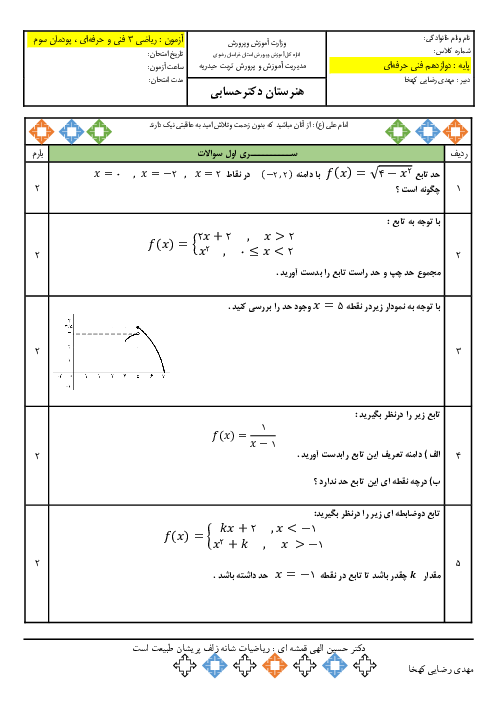
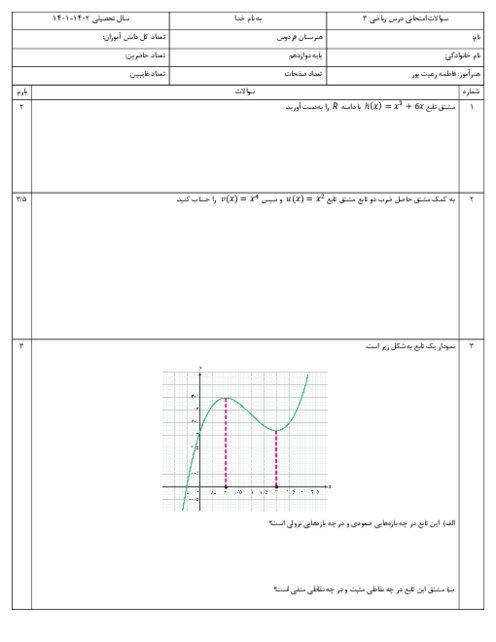
اگر $f(x) = \sin x + 2\cos x$ باشد، آنگاه حاصل $f(\frac{\pi }{3}) + f(\frac{\pi }{4}) - 1$ کدام است؟
$\frac{{\sqrt 3 + 3\sqrt 2 }}{2}$
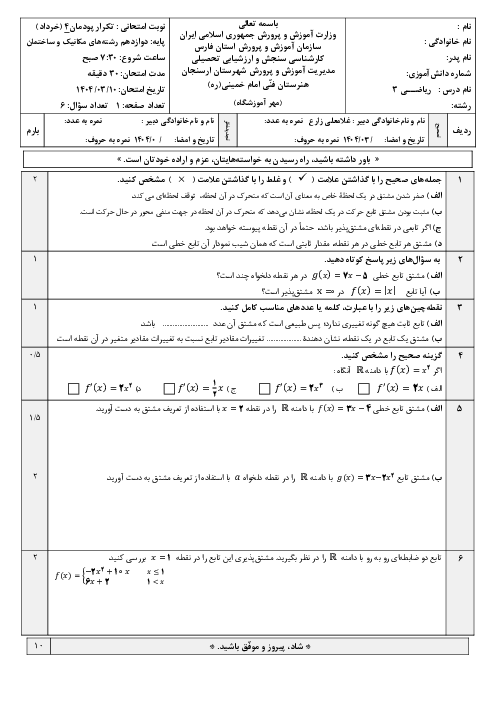
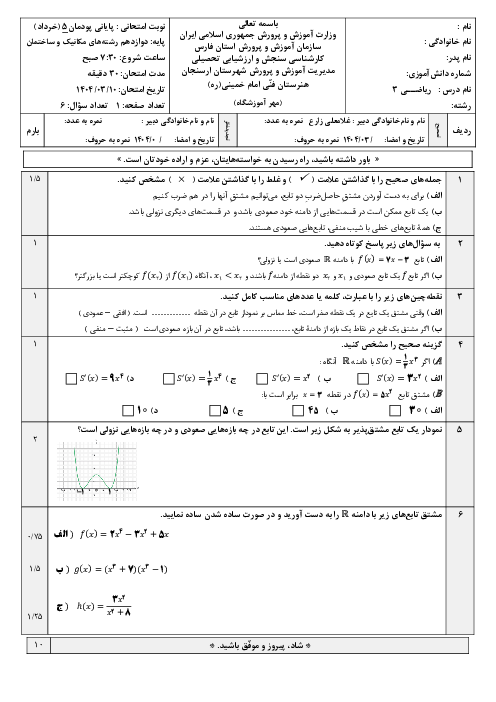
2 )
$\frac{{\sqrt 2 + 2\sqrt 3 }}{2}$
3 )
$\frac{{\sqrt 3 + \sqrt 2 - 1}}{2}$
4 )
$\frac{{\sqrt 3 + 3\sqrt 2 - 1}}{2}$
پاسخ تشریحی :
تحلیل ویدئویی تست
راضیه هادیان 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...