بزرگ‌ ترین مجموعه‌ای که در آن تابع با دامنه‌ی ، دارای حد است، کدام است؟

گاما رو نصب کن!

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

ریاضی پنجم فصل اول ریاضی ششم فصل اول الگوی مثلثی عدد شش رقمی بدون تکرار تغییر فیزیکی و شیمیایی ریاضی چهارم خط به خط زیست دهم جمله خبری نهاد چیست چه اعدادی بر ۶ بخش پذیرند مسند چیست مراحل روش علمی درس اول زبان هشتم با معنی و تلفظ

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

پودمان 2: درک مفهوم حد ریاضی3 فنی دوازدهم دوره دوم متوسطه- فنی الکترونیک (صنعت)

بزرگ‌ ترین مجموعه‌ای که در آن تابع $f(x) = \frac{{(x - {x^3})\sin (x)}}{{{x^2}(1 + x)}}$ با دامنه‌ی $R - \left\{ {0, - 1} \right\}$، دارای حد است، کدام است؟

1 )

$R - \left\{ 0 \right\}$

2 )

$R - \left\{ { - 1} \right\}$

3 )

$R - \left\{ {0, - 1} \right\}$

4 )

$R$

نمایش پاسخ

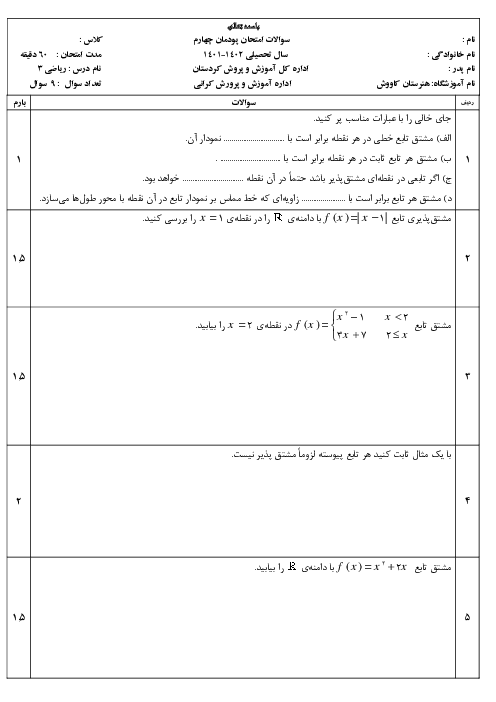
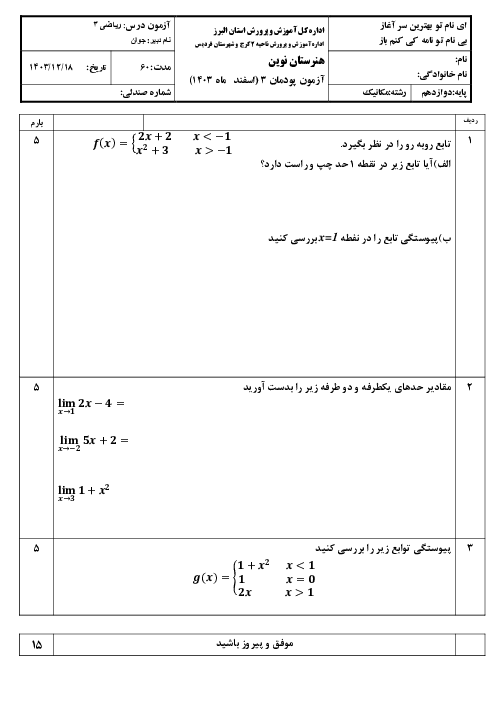
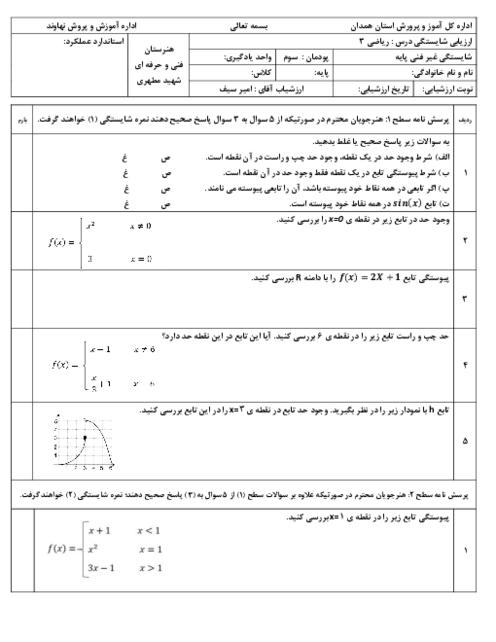
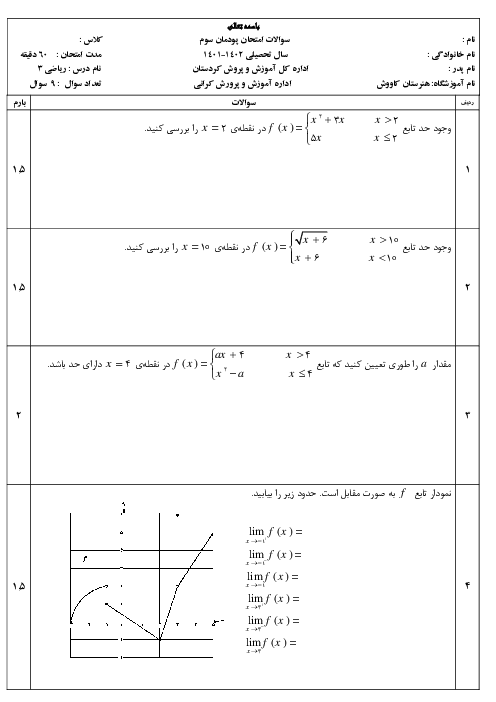
این تابع در تمام نقاط دامنه دارای حد است. این تابع ممکن است فقط در ریشه‌های مخرج حد نداشته باشد که حد آن‌ها را می‌یابیم.

$f(x) = \frac{{(x - {x^3})\sin x}}{{{x^2}(1 + x)}} = \frac{{x(1 - x)(1 + x)\sin x}}{{{x^2}(1 + x)}}$

$ = \frac{{(1 - x)\sin x}}{x}\,\,\,\,,\,x \ne 0, - 1$

$\left\{ {\begin{array}{*{20}{c}}
{\mathop {\lim }\limits_{x \to - 1} f(x) = \frac{{2\sin ( - 1)}}{{ - 1}} = - 2\sin ( - 1)\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\
{\mathop {\lim }\limits_{x \to 0} f(x) = \mathop {\lim }\limits_{x \to 0} (1 - x).\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1 \times 1 = 1}
\end{array}} \right.$

پس تابع $f$ در تمام نقاط $R$ حد دارد.

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده