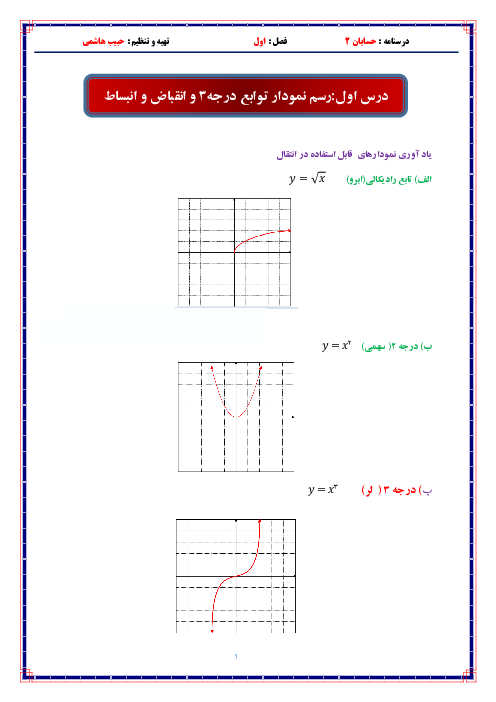
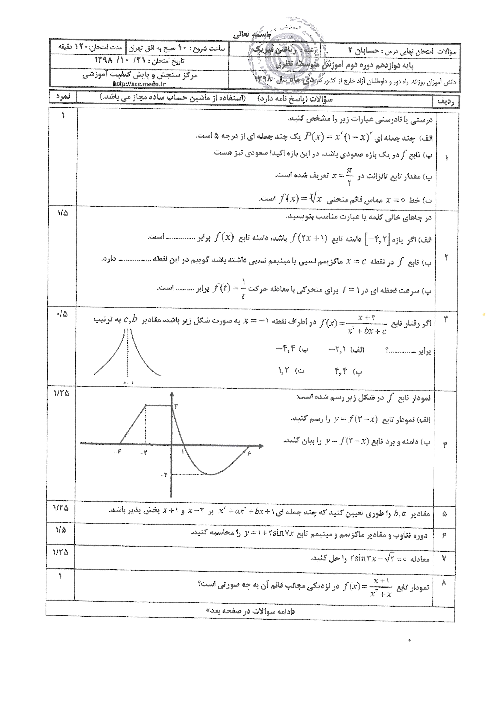
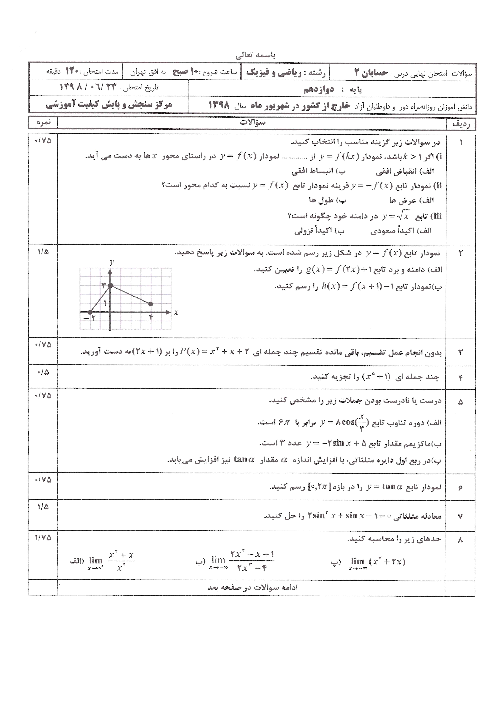
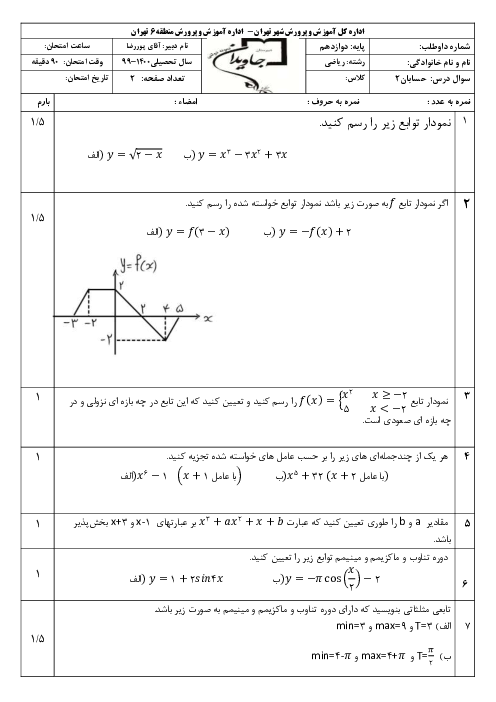
درس 1: اکسترمم‌های یک تابع و توابع صعودی و نزولی
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
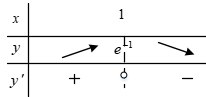
تابع $y=x{{e}^{-x}}$ در نقطهٔ بحرانی خود چه وضعیتی دارد و مقدار تابع در آن نقطه، کدام است؟
ماکزیمم و $\frac{1}{e}$
2 )
مینیمم و $\frac{1}{e}$
3 )
ماکزیمم و $e$
4 )
مینیمم و $e$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...