درس 1: آشنایی با منطق ریاضی
آمار و احتمال
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
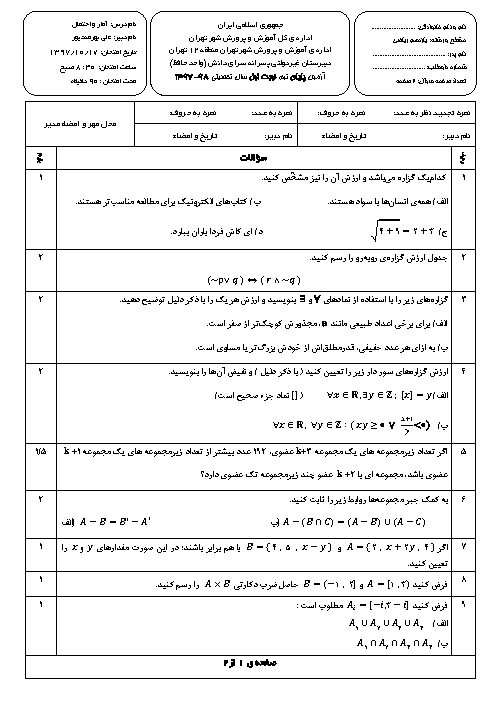
نقیض گزارهٔ $\forall x\in (-\infty ,0)\,\,\,;\,\,\,2x-\frac{1}{2x}\le -1$ چه ارزشی دارد و به چه صورت قابل‌بیان است؟
1 )
درست، $\forall x\in (-\infty ,0)\,\,\,;\,\,\,2x-\frac{1}{2x}\gt -1$
2 )
نادرست، $\exists x\in (-\infty ,0)\,\,\,;\,\,\,2x-\frac{1}{2x}\gt -1$
درست، $\exists x\in (-\infty ,0)\,\,\,;\,\,\,2x-\frac{1}{2x}\gt -1$
4 )
نادرست، $\forall x\in (-\infty ,0)\,\,\,;\,\,\,2x-\frac{1}{2x}\gt -1$
پاسخ تشریحی :
تحلیل ویدئویی تست
ریحانه نیکنام 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...