در کدام گزینه، دو گزاره همارز نیستند؟
1 )
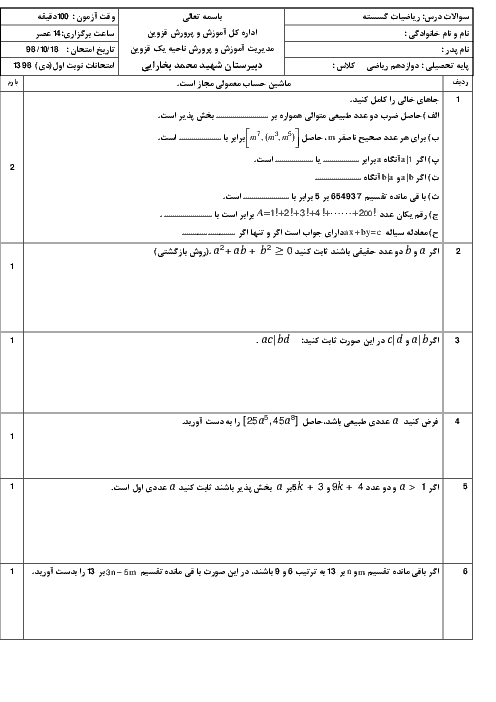
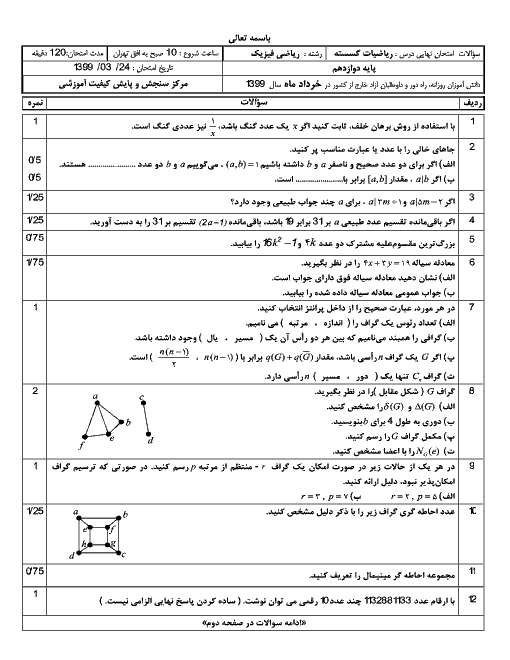
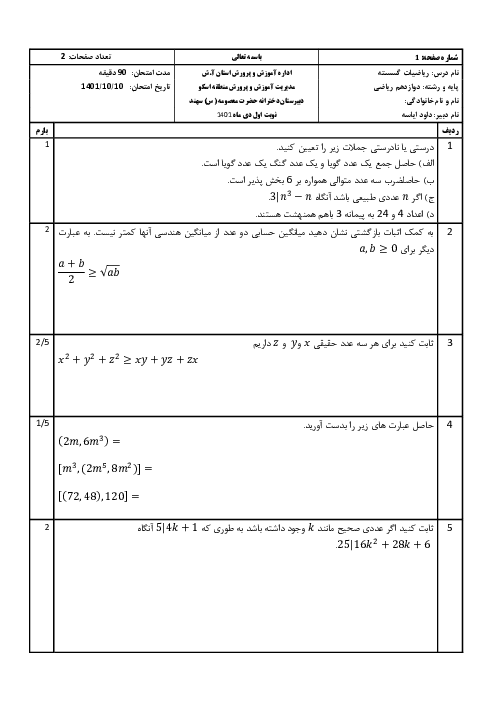
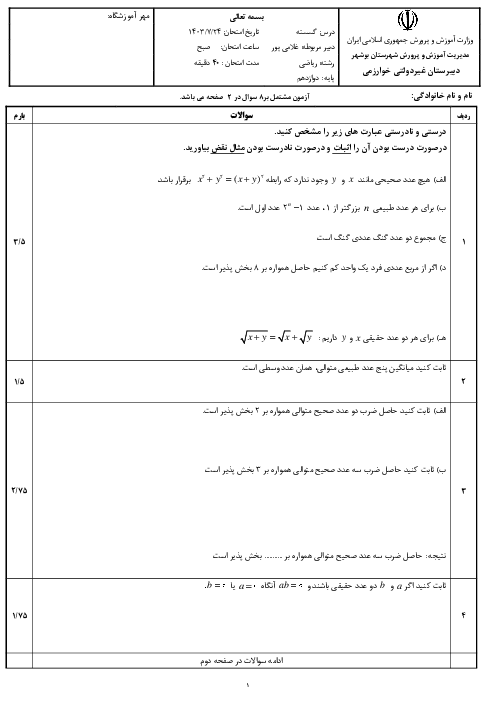
${{a}^{2}}+ab+{{b}^{2}}\ge 0$ و ${{(a+\frac{b}{2})}^{2}}+\frac{3{{b}^{2}}}{4}\ge 0$ «$a,b\in \mathbb{R}$ »
2 )
$\frac{a+b}{2}\ge \sqrt{ab}$ و ${{(\sqrt{a}-\sqrt{b})}^{2}}\ge 0$ «$a\gt 0$ و $b\gt 0$ »
3 )
$x+\frac{1}{x}\le -2$ و ${{(x+1)}^{2}}\ge 0$ «$x\lt 0$ »
$\frac{a}{{{b}^{2}}}+\frac{b}{{{a}^{2}}}\ge \frac{1}{a}+\frac{1}{b}$ و $(a+b)\ge 0$ «$a\gt 0$ و $b\gt 0$ »
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...