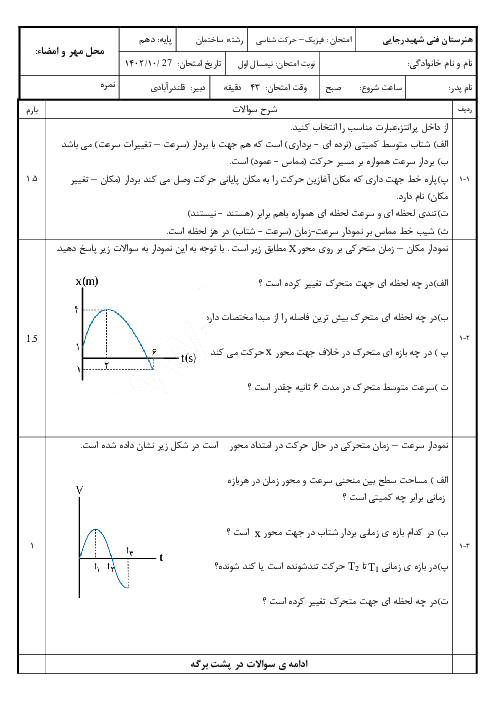
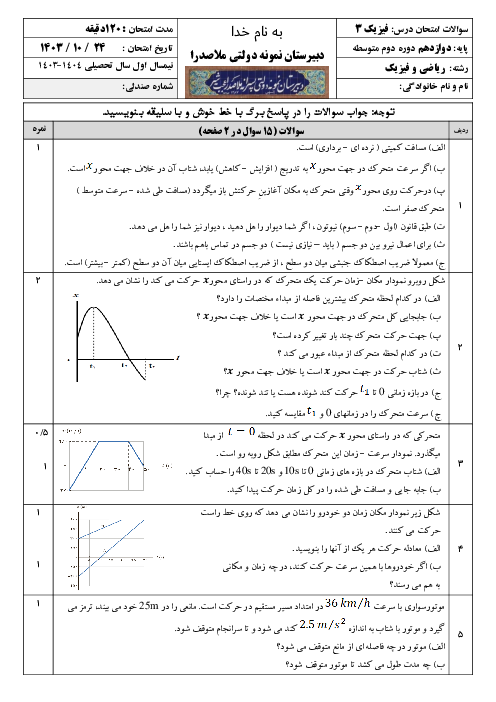
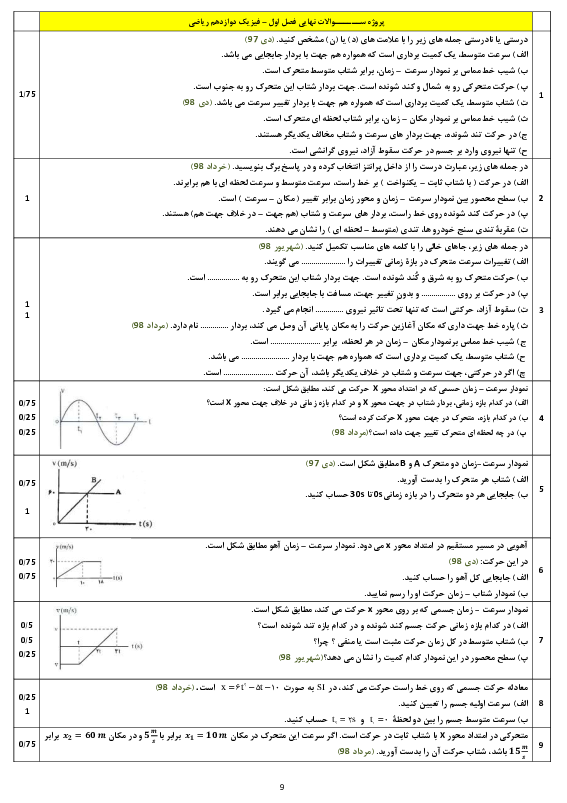
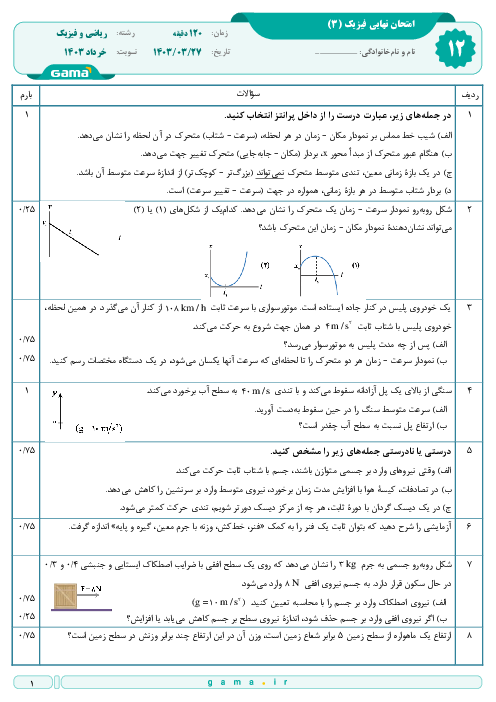
برای یافتن معادلهٔ مکان - زمان نوسانگر $B$، باید دامنه و دورهٔ تناوب آن را به‌دست آوریم. از این‌رو برای پاسخ دادن به این سؤال، گام‌های زیر را طی می‌کنیم:

گام اول:

${{x}_{A}}=\overset{{{A}_{A}}}{\mathop{0/1\pi }}\,\cos (\overset{{{\omega }_{A}}}{\mathop{\pi }}\,t)\Rightarrow {{\omega }_{A}}=\frac{2\pi }{{{T}_{A}}}=\pi \Rightarrow {{T}_{A}}=2s$

گام دوم: طبق صورت سؤال، دورهٔ تناوب نوسانگر $B$، 2 ثانیه بیشتر از نوسانگر $A$ است و داریم:

${{T}_{B}}={{T}_{A}}+2=2+2=4s\Rightarrow {{\omega }_{B}}=\frac{2\pi }{T}=\frac{2\pi }{4}=\frac{\pi }{2}{rad}/{s}\;$

گام سوم: با توجه به برابر بودن بیشینهٔ تندی دو نوسانگر، داریم:

${{V}_{{{\max }_{B}}}}={{V}_{{{\max }_{A}}}}\Rightarrow {{A}_{B}}{{\omega }_{B}}={{A}_{A}}{{\omega }_{A}}\Rightarrow {{A}_{B}}\times \frac{\pi }{2}=0/1\pi \times \pi \Rightarrow {{A}_{B}}=0/2\pi $

فرم کلی معادلهٔ مکان - زمان: ${{x}_{B}}={{A}_{B}}\cos {{\omega }_{B}}t=0/2\pi \cos \frac{\pi }{2}t$