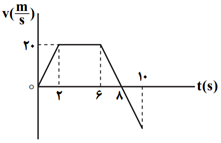
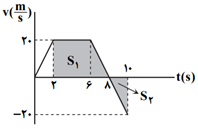
مساحت محصور به نمودار سرعت - زمان و محور زمان، (با رعايت علامت) برابر جابه‌جايی متحرک است. اگر اين مساحت به بازهٔ زمانی تقسيم شود سرعت متوسط محاسبه می‌شود. 

${{S}_{1}}=\frac{6+4}{2}\times 20=100m\Rightarrow \Delta {{x}_{1}}=+{{S}_{1}}=+100m$

برای محاسبهٔ ${{S}_{2}}$ به سرعت لحظهٔ $t=10s$ نياز است. چون شيب خط در بازهٔ زمانی $(6s,8s)$ ثابت است می‌توان اين سرعت را محاسبه نمود.

شیب $=\frac{0-20}{8-6}=-10\Rightarrow -10=\frac{{{v}_{10s}}-0}{10-8}\Rightarrow {{v}_{10s}}=-20\frac{m}{s}$

${{S}_{2}}=\frac{20\times 2}{2}=20m\Rightarrow \Delta {{x}_{2}}=-{{S}_{2}}=-20m$

$\Delta {{x}_{t}}=\Delta {{x}_{1}}+\Delta {{x}_{2}}={{S}_{1}}+(-{{S}_{2}})=100+(-20)=80m\Rightarrow {{v}_{av}}=\frac{\Delta {{x}_{t}}}{\Delta t}=\frac{80}{10-2}=10\frac{m}{s}$

برای محاسبۀ تندی متوسط بايد مسافت طی‌شده را به زمان تقسيم كنيم. ازاين‌رو مساحت ${{S}_{2}}$ را مثبت لحاظ می‌کنیم:

${{s}_{av}}=\frac{{{\ell }_{t}}}{\Delta t}=\frac{{{S}_{1}}+{{S}_{2}}}{\Delta t}=\frac{100+20}{10-2}=\frac{120}{8}=15\frac{m}{s}$