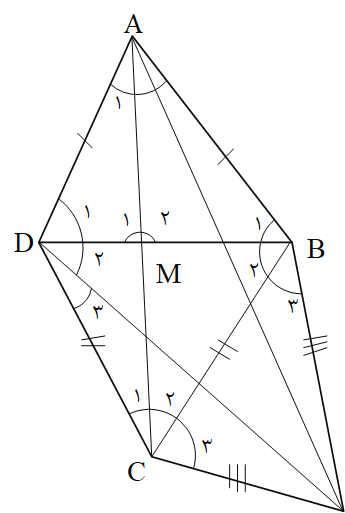
$\mathop {ABD}\limits^\Delta  :{180^ \circ } - {80^ \circ } = {100^ \circ }$

$ \Rightarrow {\hat B_1} = {\hat D_1} = {50^ \circ } \Rightarrow \hat C = {50^ \circ }$

${\hat A_1} = B\hat AM = {40^ \circ }\,,\,{\hat D_1} = {50^ \circ }$

$ \Rightarrow {\hat M_1} = {\hat M_2} = {90^ \circ }$

${\hat C_1} = {25^ \circ } \Rightarrow C\hat DB = {90^ \circ } - {25^ \circ } = {65^ \circ }$

$ \Rightarrow {\hat B_2} = {65^ \circ } \Rightarrow DC = BC$

$\left. {\begin{array}{*{20}{c}}
  {\mathop {BDC}\limits^\Delta   - \mathop {BCE}\limits^\Delta  } \\ 
  {\hat E = \hat C = {{50}^ \circ }} 
\end{array}} \right\} \Rightarrow {\hat B_3} = {\hat C_3} = 65$

$ \Rightarrow {\hat B_1} + {\hat B_2} + {\hat B_3} = {50^ \circ } + {65^ \circ } + {65^ \circ } = {180^ \circ }$

بنابراین خط AE همان خط ABE است.

$\left. {\begin{array}{*{20}{c}}
  {AED \Rightarrow \hat A = A\hat DE = {{80}^ \circ }} \\ 
  {{{\hat D}_1} = {{50}^ \circ }} 
\end{array}} \right\} \Rightarrow \left. {\begin{array}{*{20}{c}}
  {{{\hat D}_2} = {{30}^ \circ }} \\ 
  {B\hat DC = {{65}^ \circ }} 
\end{array}} \right\} \Rightarrow E\hat DC = {35^ \circ }$