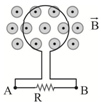
برای تعيين جهت جريان القايی می‌توان گفت طبق رابطهٔ $\Phi ={{t}^{2}}-16$ در لحظهٔ $t=4s$ شار مغناطيسی صفر می‌شود. بنابراين در بازهٔ زمانی $t=0$ تا $t=4s$، اندازهٔ شار مغناطيسی گذرا از حلقه كاهش می‌یابد كه ناشی از كاهش اندازهٔ ميدان مغناطيسی برون‌سوی عبوری از داخل حلقه است. لذا بايد جريان القايی در حلقه در جهتی باشد كه ميدان مغناطيسی ناشی از آن هم‌جهت با ميدان مغناطيسی خارجی، يعنی برون‌سو باشد. بنابراين جريان القايی در حلقه پادساعتگرد است كه در مقاومت $R$ از $A$ به $B$ می‌باشد. اكنون برای محاسبهٔ بزرگی نيروی محركه القايی در ثانيهٔ دوم داريم:

$\Phi ={{t}^{2}}-16\Rightarrow \left\{ \begin{matrix} t=1s\Rightarrow {{\Phi }_{1}}=-15Wb  \\ t=2s\Rightarrow {{\Phi }_{2}}=-12Wb  \\ \end{matrix} \right.$

$\left| \overline{\varepsilon } \right|=\left| -N\frac{\Delta \Phi }{\Delta t} \right|\xrightarrow{N=1}\left| \overline{\varepsilon } \right|=\left| (1)\frac{-12-(-15)}{2-1} \right|=3V$