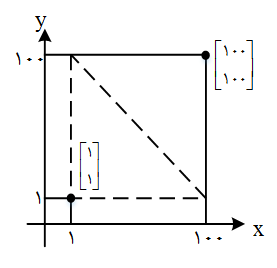
مجموعهٔ زیر را که مجموعهٔ همهٔ نقاط صفحه با مختصات طبیعی است، در نظر بگیرید.
$\left\{ {\left[ {\begin{array}{*{20}{c}}
x \\
y
\end{array}} \right]|x,y \in \mathbb{N}} \right\}$
چه تعداد از نقاط این مجموعه به نقطهٔ $\left[ {\begin{array}{*{20}{c}}
1 \\
1
\end{array}} \right]$ نزدیک‌تر هستند تا به نقطهٔ $\left[ {\begin{array}{*{20}{c}}
{100} \\
{100}
\end{array}} \right]$؟
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...