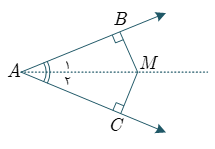
با تکمیل استدلال زیر ثابت کنید: «هر نقطه که روی نیمساز یک زاویه باشد، از دو ضلع زاویه به یک فاصله است.»
$\left. \begin{align}
& \hat{B}=\hat{C}={{90}^{\circ }}\, \\
& ......=...... \\
& ......=......\, \\
\end{align} \right\}\xrightarrow{\begin{matrix}
{} & {} & {} & {} \\
\end{matrix}}\overset{\Delta }{\mathop{AMB}}\,\cong \overset{\Delta }{\mathop{AMC}}\,\Rightarrow \overline{MB}=\overline{MC}$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...