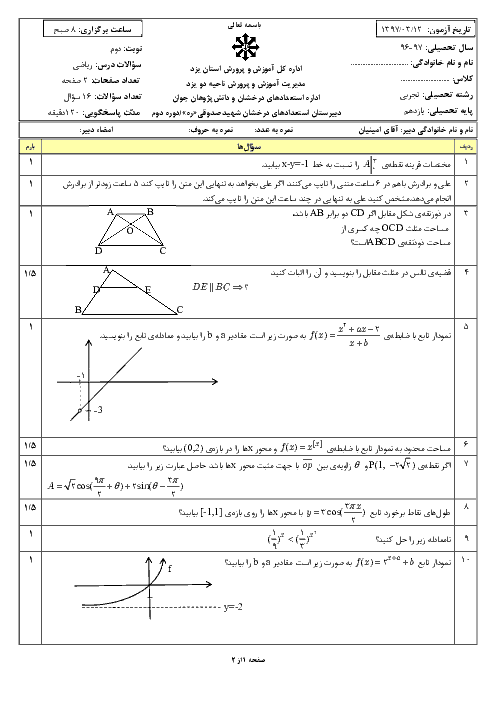
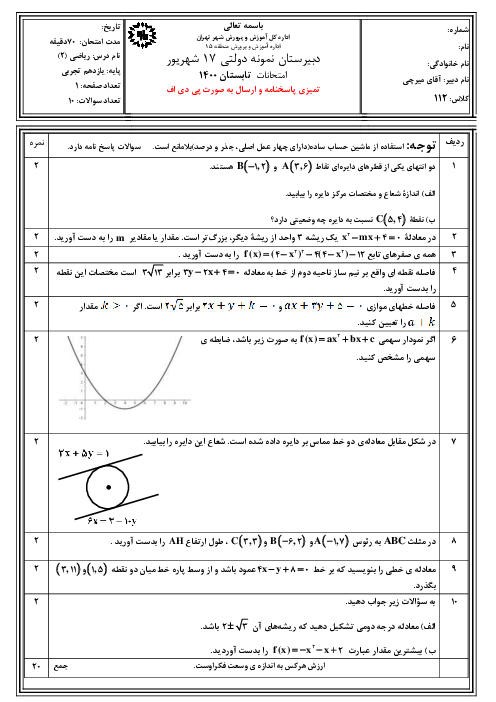
درس 1: واحدهای اندازه گیری زاویه
ریاضی (2)
یازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
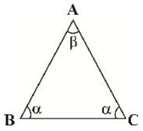
در يک مثلث متساوی‌الساقين، مجموع دو زاويهٔ نابرابر $\frac{360}{\pi }$ درجه است. اندازهٔ زاويهٔ كوچكتر بر حسب راديان تقريباً كدام است؟ $(\pi \simeq 3/14)$
تحلیل ویدئویی تست
محسن ذوالفقاری 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...