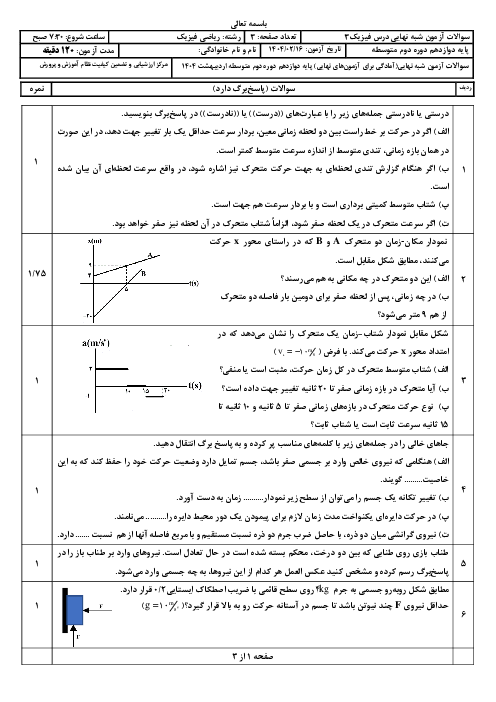
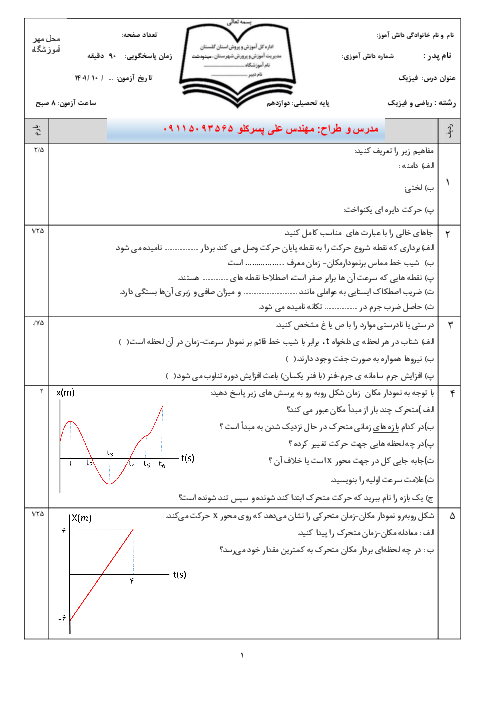
نیروی کشسانی فنر، نیروی مرکزگرای لازم جهت دوران یکنواخت جسم روی سطح افقی بدون اصطکاک را تأمین می‌کند. اگر طول اولیه‌ی فنر را ${{L}_{1}}$ و تغییر طول آن‌را $x$ در نظر بگیریم، شعاع حرکت دایره‌ای برابر با ${{L}_{2}}={{L}_{1}}+x$ خواهد بود. با استفاده از قانون دوم نیوتون و قانون هوک داریم:

${{F}_{net}}=m\frac{{{v}^{2}}}{r}\xrightarrow{v=\frac{2\pi r}{T}}{{F}_{net}}=4{{\pi }^{2}}\frac{mr}{{{T}^{2}}}\xrightarrow[r={{L}_{2}}={{L}_{1}}+x]{{{F}_{net}}=kx}kx=4{{\pi }^{2}}\frac{m\left( {{L}_{1}}+x \right)}{{{T}^{2}}}$

$\Rightarrow 150x=4{{\pi }^{2}}\times \frac{0/1\left( {{L}_{1}}+x \right)}{{{\left( \frac{\pi }{5} \right)}^{2}}}\Rightarrow 15x={{L}_{1}}+x\Rightarrow \frac{x}{{{L}_{1}}}=\frac{1}{14}$