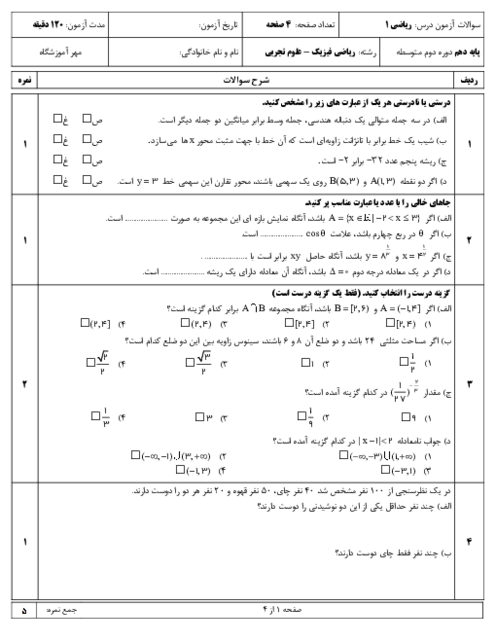
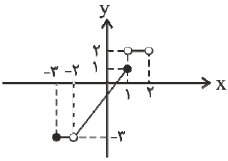
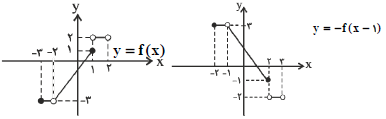اگر نمودار تابع $f(x)$ به‌صورت زير باشد، دامنه و برد تابع $y=-f(x-1)$ به‌ترتیب از راست به چپ کدامند؟
1 )
${{R}_{f}}=\left[ -1,3 \right],{{D}_{f}}=\left[ -2,3 \right)-\left\{ 1 \right\}$
${{R}_{f}}=\left[ -1,3 \right]\cup \left\{ -2 \right\},{{D}_{f}}=\left[ -2,3 \right)-\left\{ -1 \right\}$
3 )
${{R}_{f}}=\left[ -1,3 \right]\cup \left\{ -2 \right\},{{D}_{f}}=\left( -2,3 \right]-\left\{ -1 \right\}$
4 )
${{R}_{f}}=\left[ -1,3 \right],{{D}_{f}}=\left( -2,3 \right]-\left\{ 1 \right\}$
پاسخ تشریحی :
تحلیل ویدئویی تست
زهرا شیخ الاسلامی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...