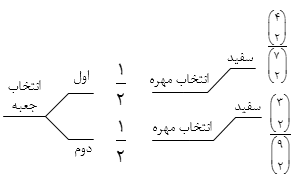
در جعبهٔ اول $4$ مهرهٔ سفید و $3$ مهرهٔ سیاه و در جعبهٔ دوم $3$ مهرهٔ سفید و $6$ مهرهٔ سیاه موجود است. به تصادف یکی از جعبه‌ها را انتخاب کرده و دو مهره با هم از آن بیرون می‌آوریم. با کدام احتمال هر دو مهره سفید است؟
$\frac{31}{168}$
2 )
$\frac{11}{56}$
3 )
$\frac{17}{84}$
4 )
$\frac{13}{56}$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...