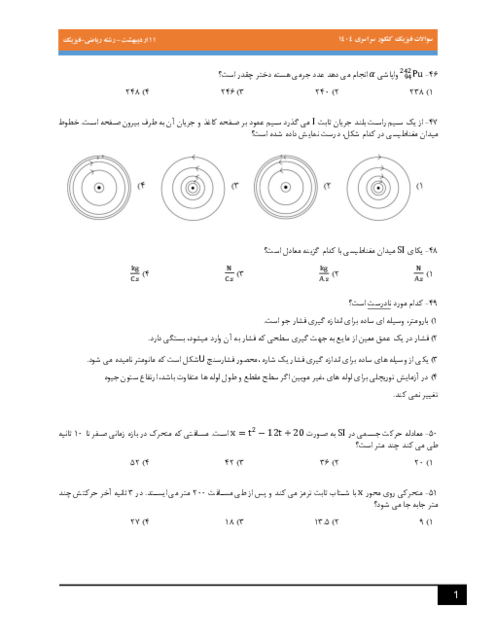
در شکل زیر، میدان الکتریکی حاصل از بار ${{q}_{1}}$ در محل بار ${{q}_{2}}$، ${{\overrightarrow{E}}_{1}}$ است و میدان الکتریکی حاصل از بار ${{q}_{2}}$ در محل بار ${{q}_{1}}$، ${{\overrightarrow{E}}_{2}}$ است. کدام رابطه بین ${{\overrightarrow{E}}_{1}}$ و ${{\overrightarrow{E}}_{2}}$ برقرار است؟
1 )
${{\overrightarrow{E}}_{2}}={{\overrightarrow{E}}_{1}}$
${{\overrightarrow{E}}_{2}}=4{{\overrightarrow{E}}_{1}}$
3 )
${{\overrightarrow{E}}_{2}}=-{{\overrightarrow{E}}_{1}}$
4 )
${{\overrightarrow{E}}_{2}}=-4{{\overrightarrow{E}}_{1}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...