درس 1: آشنایی با برخی از انواع توابع
ریاضی (2)
یازدهم
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
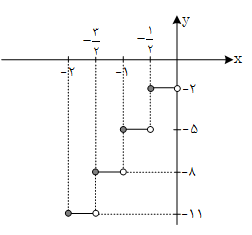
نمودار تابع $f(x)=3\left[ 2x \right]+1$ با دامنهی $\left[ -2,0 \right)$، از چند پله تشکیل شده و طول هر پله چند واحد است؟
4 پله به طول $\frac{1}{2}$ واحد
2 )
2 پله به طول 1 واحد
3 )
3 پله به طول $\frac{2}{3}$ واحد
4 )
1 پله به طول 2 واحد
پاسخ تشریحی :