درس 4: قدر مطلق و ویژگی‌های آن
حسابان (1)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
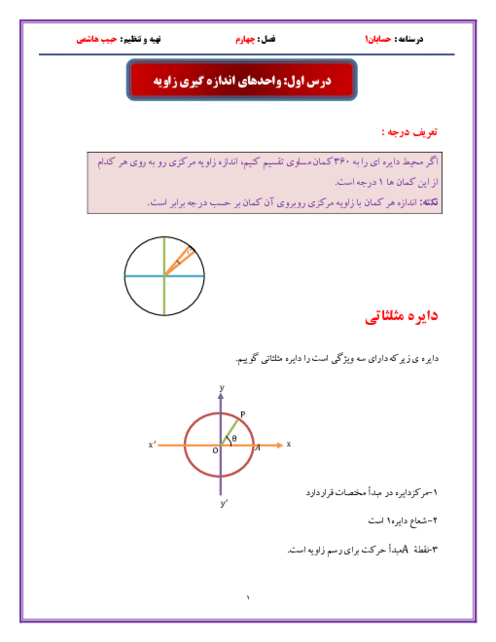
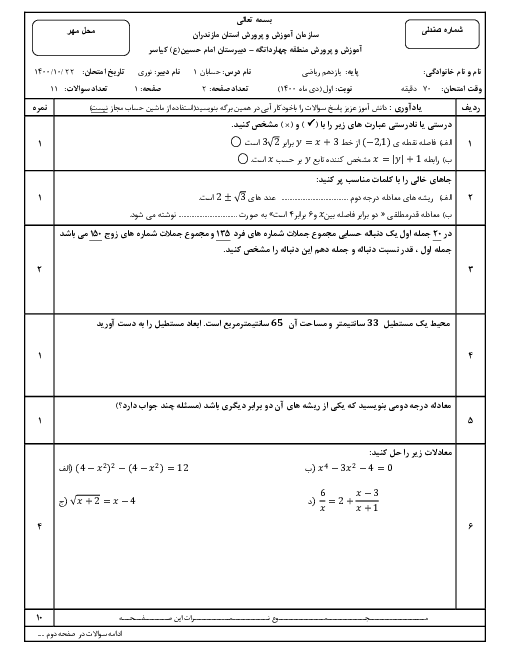
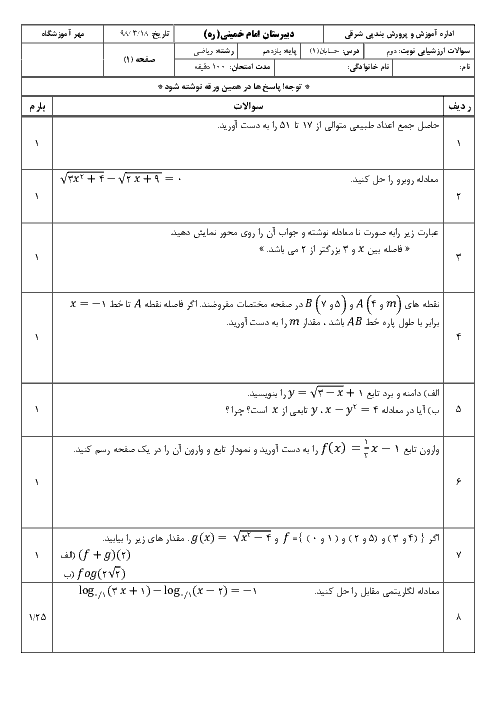
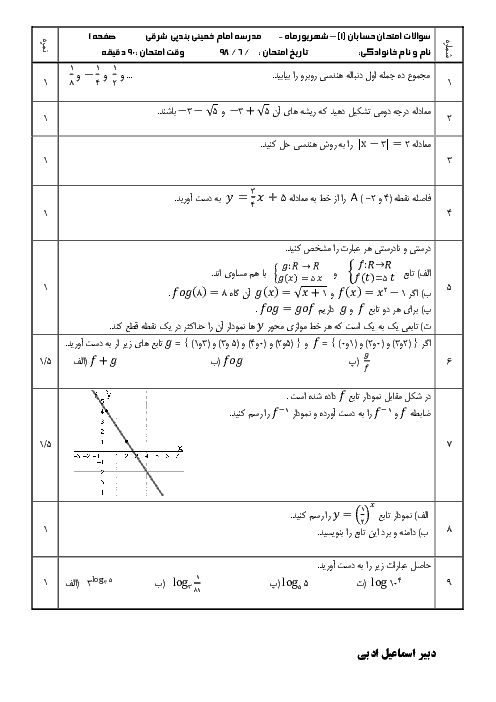
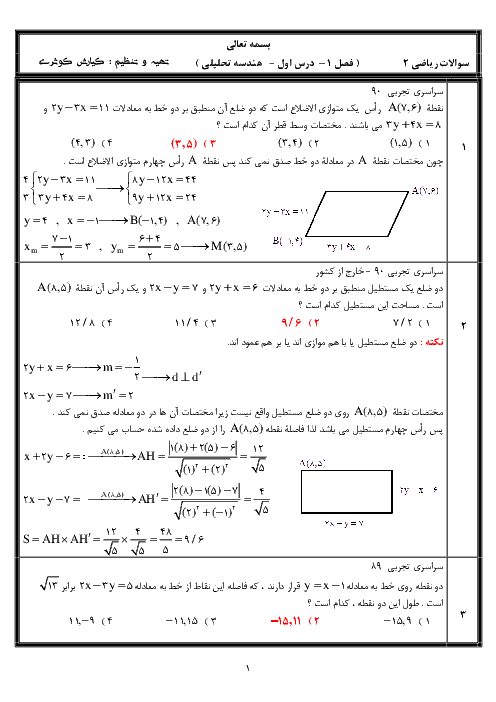
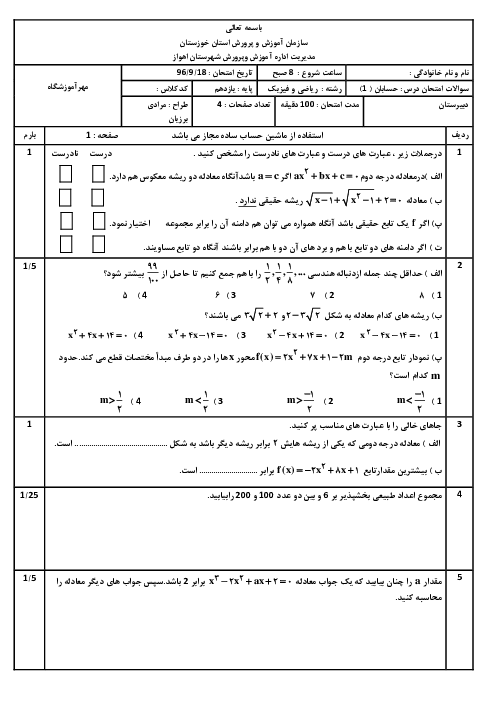
مجموعهٔ جواب x برای برقراری تساوی $\left| {{x}^{2}}+2x+2 \right|=\left| {{x}^{2}}+x+1 \right|+\left| x+1 \right|$ کدام است؟
$\left\{ x\text{ }\!\!|\!\!\text{ }x\ge -1 \right\}$
2 )
$\left\{ x\text{ }\!\!|\!\!\text{ }x\le -1 \right\}$
3 )
$\left\{ x\text{ }\!\!|\!\!\text{ }x\ge 1 \right\}$
4 )
$\left\{ x\text{ }\!\!|\!\!\text{ }x\le 1 \right\}$
پاسخ تشریحی :
تحلیل ویدئویی تست
مهدی خلجی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...