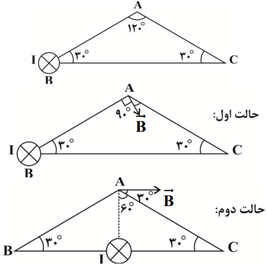
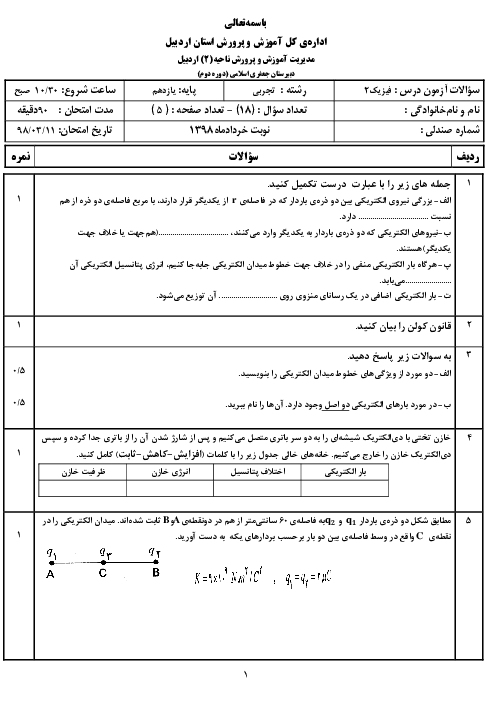
مطابق شكل زير، جريان الكتريكی درون‌سوی $I$، عمود بر صفحه از رأس $B$ واقع در مثلث $ABC$ می‌گذرد. با جابه‌جايی اين سيم به وسط ضلع $BC$، جهت بردار ميدان مغناطيسی اين سيم در رأس $A$ چند درجه تغيير می‌كند؟ $(\overline{AB}=\overline{AC})$