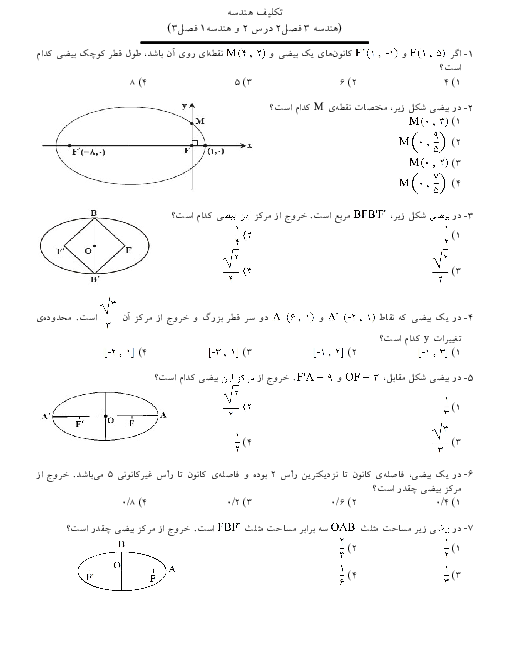
دنبالهٔ ${a_n} = \left\{ {\begin{array}{*{20}{c}} {{2^k}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,n = 3k} \\ { - 2k + 4\,\,\,\,\,\,\,\,\,\,\,\,;\,\,\,\,\,\,\,\,\,\,n = 3k + 1} \\ {\left[ {\frac{n}{{k + 2}}} \right] + a\,\,\,\,\,;\,\,\,\,\,\,\,\,\,\,n = 3k + 2} \end{array}} \right.\,$ به ازای اعداد حسابی $n$، مفروض است. اگر مجموع 10 جملهٔ اول این دنباله 19 باشد، حاصل عبارت $a_2 + a_5 + a_8 + ... + a_{29}$، کدام است؟
2-
2 )
صفر
3 )
2
4 )
1
تحلیل ویدئویی تست
محسن ذوالفقاری 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...