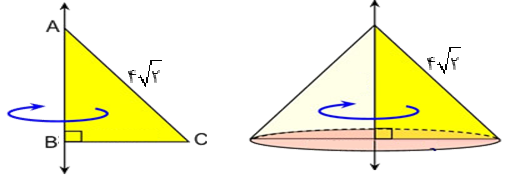
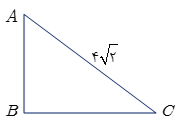
مثلث قائم‌الزاویه متساوی‌الساقین زیر را حول یکی از اضلاع زاویهٔ قائمهٔ آن دوران می‌دهیم. حجم جسم حاصل چند سانتی‌متر مکعب خواهد شد؟ (اندازهٔ وتر مثلث $4\sqrt 2 $ سانتی‌متر است.)
$\frac{{64\pi }}{3}$
2 )
$\frac{{128\pi }}{3}$
3 )
$\frac{{32\pi }}{3}$
4 )
$\frac{{12\pi }}{3}$
پاسخ تشریحی :
تحلیل ویدئویی تست
عادل علی پناه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...