پودمان 2: تابع‌های خطی و درجۀ دوم و کاربرد آنها در حل معادله‌ها و نامعادله‌ها
ریاضی2 فنی
یازدهم
دوره دوم متوسطه- فنی
مشترک شاخۀ فنی و حرفه‌ای
درسنامه آموزشی این مبحث
به ازای کدام مقادیر $m$ نمودار تابع $f(x) = 2{x^2} + (m - 1)x + m - \frac{5}{2}$، محور $x$ها را در دو نقطه‌ی متمایز قطع می‌کند؟
1 )
$2 \lt m \lt 5$
2 )
$3 \lt m \lt 7$
$m \gt 7$ یا $m \lt 3$
4 )
$m \gt 5$ یا $m \lt 3$
پاسخ تشریحی :
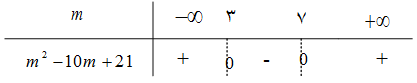
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...