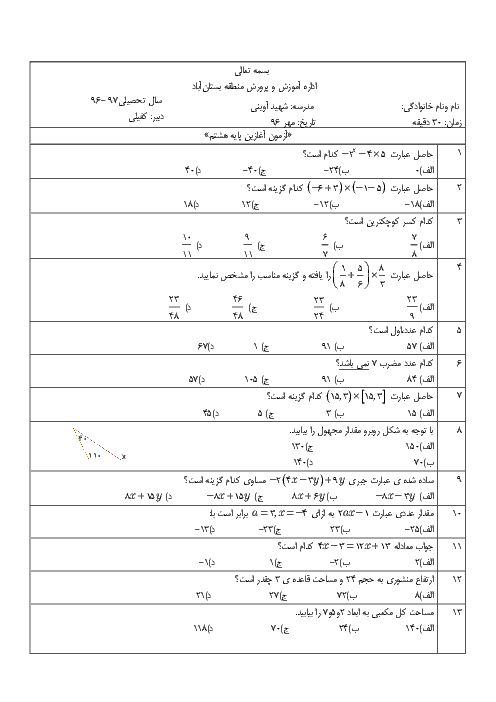
اگر نیم‌ساز داخلی زاویهٔ $A$ از مثلث $ABC$ با نیم‌ساز خارجی زاویهٔ $C$ از آن مثلث، زاویهٔ ${{20}^{{}^\circ }}$ بسازد، زاویهٔ بین نیم‌سازهای داخلی زاویه‌های $A$ و $C$ از مثلث کدام است؟
1 )
${{100}^{{}^\circ }}$
${{110}^{{}^\circ }}$
3 )
${{90}^{{}^\circ }}$
4 )
${{80}^{{}^\circ }}$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...