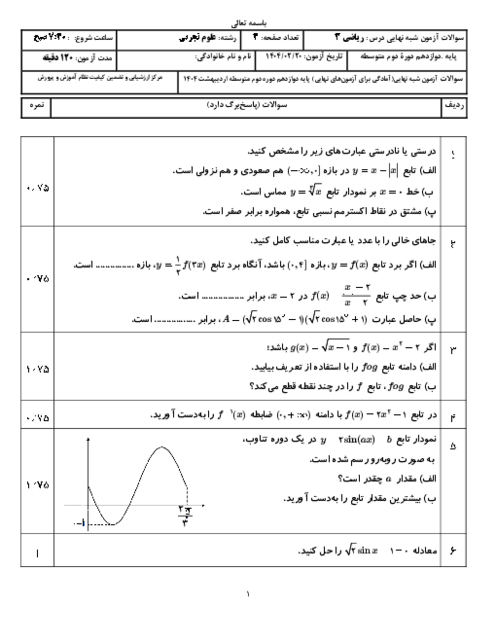
ابتدا در تابع $f(x)$، به جای $x$، $g(x)$ را جایگذاری میکنیم و آن را با تابع $(fog)(x)$ که در صورت سؤال داده شده است، قرار میدهیم و $g(x)$ را حساب میکنیم:
$(fog)(x)=f(g(x))={{g}^{2}}(x)-4g(x)+3={{x}^{2}}+3x+\frac{5}{4}$
در دو سمت رابطهٔ فوق مربع کامل تشکیل میدهیم:
$\Rightarrow {{(g(x)-2)}^{2}}-4+3={{(x+\frac{3}{2})}^{2}}-\frac{9}{4}+\frac{5}{4}$
$\Rightarrow {{(g(x)-2)}^{2}}-1={{(x+\frac{3}{2})}^{2}}-1$
(شکل)
برای به دست آوردن $g(f(x))$، در تابع $g(x)$، به جای $x$، $f(x)$ را قرار میدهیم:
$g(f(x))=f(x)+\frac{7}{2}={{x}^{2}}-4x+3+\frac{7}{2}={{x}^{2}}-4x+\frac{13}{2}$