فاصلهٔ نقطهٔ ماکسیمم نسبی و یک نقطهٔ عطف منحنی به معادلهٔ کدام است؟

گاما رو نصب کن!

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

ریاضی پنجم فصل اول ریاضی ششم فصل اول الگوی مثلثی عدد شش رقمی بدون تکرار تغییر فیزیکی و شیمیایی ریاضی چهارم خط به خط زیست دهم جمله خبری نهاد چیست چه اعدادی بر ۶ بخش پذیرند مسند چیست مراحل روش علمی درس اول زبان هشتم با معنی و تلفظ

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

تعداد مشاهده رایگان باقی مانده: 2 صفحه

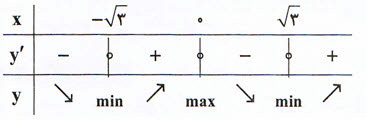
درس 2: جهت تقعر نمودار یک تابع و نقطۀ عطف آن حسابان (2) دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

فاصلهٔ نقطهٔ ماکسیمم نسبی و یک نقطهٔ عطف منحنی به معادلهٔ $y={{x}^{4}}-6{{x}^{2}}+5$ کدام است؟

1 )

$\sqrt{10}$

2 )

$\sqrt{13}$

3 )

$\sqrt{17}$

4 )

$\sqrt{26}$

نمایش پاسخ

$y'=4{{x}^{3}}-12x=0\to y'=4x({{x}^{2}}-3)=0$

$\to x=0,x=\sqrt{3},x=-\sqrt{3}$

با آزمون مشتق‌ اول نقطهٔ ماکسیمم نسبی را می‌یابیم:

پس $x=0$ طول ماکزیمم نسبی است.

بنابراین نقطهٔ $A(0,5)$، ماکسیمم نسبی تابع است، حال نقطهٔ عطف را می‌یابیم:

$y''=0\to 12{{x}^{2}}-12=0\Rightarrow {{x}^{2}}=1\Rightarrow x=1,x=-1$

بنابراین $B(1,0)$ یکی از نقاط عطف است و فاصلهٔ $A$ و $B$ برابر است با:

$AB=\sqrt{{{(1-0)}^{2}}+{{(0,-5)}^{2}}}=\sqrt{26}$

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

1403/03/30

عباس ابراهیمی علویجه

محتوای متنی دوره آموزشی، حسابان (2) دوازدهم دوره دوم متوسطه- نظری

مدرس: جابر عامری

مدت دوره: 220 صفحه (5 فایل)

با آلبوم تست، آزمون دلخواهتو بساز

سوپراستار

72 صفحه

بسته ویژه نمره بیست: 15 دوره امتحان نهایی درس حسابان (2) دوازدهم

ويژه نامه نوبت اول و…

سوپراستار

8 صفحه

4 سری نمونه سؤال آمادگی امتحان نهایی (نوبت دوم) حسابان (2) دوازدهم ریاضی

کلاس دوازدهمی‌ها

4 صفحه

نمونه سوال پيشنهادی امتحان نوبت دوم حسابان (2) دوازدهم دبیرستان حضرت فاطمه…

فائزه ربیعی

2 صفحه

سوالات امتحان حسابان 2 دوازدهم دبیرستان فرزانگان | نوبت اول دیماه 1400

مریم عبدالملکی

7 صفحه

نمونه سوال آمادگی امتحان نوبت دوم حسابان دوازدهم دبیرستان سید الشهداء

امیر علی سلطانی

7 صفحه

امتحان حسابان 2 پایه دوازدهم نوبت دی 1402 دبیرستان غیرانتفاعی ثامن

امین افدیده

رایـــــگان

4 صفحه

سؤالات امتحان نهایی درس حسابان (2) دوازدهم رشته ریاضی | خرداد 1398

امتحان نهایی

22 صفحه

جزوه دست نویس حسابان 2 - فصل 3

محمد شاهسون

18 صفحه

سئوالات موضوعی نهایی فصل چهارم درس حسابان2 | مشتق

جابر عامری

2 صفحه

امتحان فصل اول حسابان 2 دوازدهم دبیرستان بعثت کلاچای | تابع

محمد پاک نژاد

موارد بیشتر

ارسال فایل

تابع f(x)= 2√x-2 - k √x-1 یکنوا است. حدود k کدام است؟

در مورد فرمول انبساط و انقباض عمودی

دوره تناوب توابع سینوسی و کسینوسی

موارد بیشتر

ارسال پرسش

موارد بیشتر

جستجوهای پرتکرار

پاسخ تشریحی :

تحلیل ویدئویی تست

با آلبوم تست

نمونه سوالات مشابه

اطلاع از تغییرات در بسته‌های گاما

کاربر عزیز سلام!

پاسخ تشریحی :

تحلیل ویدئویی تست

با آلبوم تست

نمونه سوالات مشابه